如图7-6-10所示,在一个很长的斜面上的某处A,水平抛出一个物体.已知物体抛出时的动能为1.5 J,斜面的倾角θ=30°.空气阻力不计,求它落到斜面上B点时的动能.
图7-6-10
图7-6-10所示,是简化后的跳台滑雪的雪道示意图.整个雪道由倾斜的助滑雪道AB和着陆雪道DE,以及水平的起跳平台CD组成,AB与CD圆滑连接.
运动员从助滑雪道AB上由静止开始,在重力作用下,滑到D点水平飞出,不计飞行中的空气阻力,经2 s在水平方向飞行了60 m,落在着陆雪道DE上.已知从B点到D点运动员的速度大小不变.(g取10 m/s2)求:
(1)运动员在AB段下滑到B点的速度大小;
(2)若不计阻力,运动员在AB段下滑过程中下降的高度.
(3)若运动员的质量为60 kg,在AB段下降的实际高度是50 m,此过程中他克服阻力所做的功.
如图7-6-9所示,小球用不可伸长的长度为l的轻绳悬于O点,小球A在最低点需获得多大的速度才能在竖直平面内做完整的圆周运动?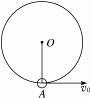
图7-6-9
如图所示,甲图中物体A从高H处由静止开始下落.乙图中物体B与C通过光滑轻滑轮用细绳相连,C放在光滑水平桌面上,C的质量是B的一半,物体B也从H高处由静止下落.求这两种情况下,A、B离地面的高度h为多少时,其动能等于势能?(设C尚未离开桌面)
如图所示,在一长为2l的不可伸长的轻杆的两端,各固定一质量为2m与m的A、B两小球,系统可绕过杆的中点O且垂直纸面的固定转轴转动.初始时轻杆处于水平状态,无初速释放后,轻杆转动.当轻杆转至竖直位置时,小球A的速率多大?
如右图所示,一根不可伸长的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直平面内绕O点摆动.现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时,细线承受的拉力是多大?
一小物块以速度v0="10" m/s沿光滑地面滑行,然后沿光滑曲面上升到顶部水平的高台上并由高台上飞出,如图7-7-17所示.问高台的高度多大时,小物块飞行的水平距离s最大?这个距离是多少?(g取10 m/s2)
图7-7-17
如图7-7-16所示,光滑圆管轨道ABC,其中AB部分平直,BC部分是处于竖直平面的、半径为R的半圆.圆管截面的半径r<<R.有一质量为m、半径比r略小的光滑小球以水平初速度v0从A点射入圆管.问:
图7-7-16
(1)若要小球能从C端出来,初速度v0需多大?
(2)在小球从C端出来的瞬间,对管壁作用力有哪几种典型情况?初速度v0各应满足什么条件?
如图7-7-13所示,一均匀铁链长L,平放在距地面为h=2L的光滑水平桌面上,其长度的 悬垂于桌面下.从静止开始释放铁链,求铁链的下端刚要着地时的速度.
悬垂于桌面下.从静止开始释放铁链,求铁链的下端刚要着地时的速度.
图7-7-13
长为L的细绳固定在O点,另一端系一质量为m的小球,开始时绳与水平方向成30°角,如图7-7-15所示.求小球由静止释放后运动到最低点C时的速度.
图7-7-15
如图7-7-12所示,质量为m的木块放在光滑的水平桌面上,用轻绳绕过桌边光滑的定滑轮与质量为2m的砝码相连,让绳拉直后使砝码从静止开始下降h的距离时,砝码未落地,木块仍在桌面上.求:
图7-7-12
(1)这时砝码的速率为多大?
(2)上述过程中砝码克服绳子拉力做的功为多少?
如图7-7-11所示,两个物体用轻绳经光滑的滑轮拴在一起,质量分别为m1、m2,m2在地面上,m1离地的高度为h,m1>m2,由静止释放.则m1落地后,m2还能上升的高度为多少?
图7-7-11
如图7-7-10所示,质量分别为m和2m的两个小物体可视为质点,用轻质细线连接,跨过光滑圆柱体,轻的着地,重的恰好与圆心一样高.若无初速度地释放,则物体m上升的最大高度为多少?
图7-7-10
据测算结果知,背越式过杆时,优秀运动员腾起的重心高度比实际过杆高度低4.1%.
按统计规律,人的重心高度约为身高的0.618倍.我国著名运动员朱建华,体重75 kg、身高1.9 m,若他起跳时重心下降0.37 m,则当他跳过Hmax="2.39" m高度而创造世界纪录时,起跳的竖直速度不小于多少?