高中物理爱因斯坦质能方程试题

（1）一静止的铝原子核 ${}_{13}{}^{27}Al$ 俘获一速度为 $\text{1.0}\times {\text{10}}^7\mathrm{m}/\mathrm{s}$ 的质子p后，变为处于激发态的硅原子核 ${}_{14}{}^{28}Si$ ，下列说法正确的是_________

A．	核反应方程为 $\text{P+}{}_{13}{}^{27}Al\text{→}{}_{14}{}^{28}Si$
B．	核反应方程过程中系统动量守恒
C．	核反应过程中系统能量不守恒
D．	核反应前后核子数相等，所以生成物的质量等于反应物的质量之和
E．	硅原子核速度的数量级为 ${\text{10}}^5\mathrm{m}/\mathrm{s}$ ，方向与质子初速度方向一致

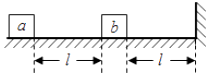
（2）如图所示，水平地面上有两个静止的小物块a和b，其连线与墙垂直：a和b相距l；b与墙之间也相距l；a的质量为m，b的质量为 $\frac{3}{4}m$ ，两物块与地面间的动摩擦因数均相同，现使a以初速度 $v_0$ 向右滑动，此后a与b发生弹性碰撞，但b没有与墙发生碰撞，重力加速度大小为g，求物块与地面间的动摩擦力因数满足的条件。

(1)我国科学家经过艰苦努力，率先建成了世界上第一个全超导托克马克试验装置并调试成功．这种装置被称为“人造太阳”，它能够承受上亿摄氏度高温且能够控制等离子态的核子发生聚变并稳定持续地输出能量，就像太阳一样为人类提供无限清洁能源．在该装置内发生的核反应方程是H＋H―→He＋X，其中粒子X的符号是________．已知H的质量是m₁， H的质量是m₂，He的质量是m₃，X的质量是m₄，光速是c，则发生一次上述聚变反应所释放的核能表达式为___________________________________________．
(2)光滑水平面上静止放置一长方形木板B，B的质量为M＝2 kg，B的右端离竖直墙6 m．现有一小物体A，其质量m＝1 kg，以v₀＝6 m/s的速度从B的左端水平滑上B，如图所示．A和B之间的动摩擦因数μ＝0.4，B与墙碰撞时间极短，且碰撞时无能量损失．要使A最终不脱离B，B的最短长度是多少？

海水中含有丰富的氘，完全可充当未来的主要能源。两个氘核的核反应为：+→+n，其中氘核的质量为2.013u，氦核的质量为3.0150u，中子的质量为1.0087u.(1u=931.5Mev).
求核反应中释放的核能；
在两个氘核以相等的动能0.35MeV进行对心碰撞，并且核能全部转化为机械能的情况下，求反应中产生的中子和氦核的动能。

太空中的射线暴是从很远的星球发射出来的，当射线暴发生时，数秒内释放的能量大致相当于当前太阳质量全部发生亏损所释放的能量。已知太阳光从太阳到地球需要时间为，地球绕太阳公转的周期为，真空中的光速为，万有引力常量为。
（1）根据以上给出的物理量写出太阳质量M的表达式。
（2）推算一次射线暴发生时所释放的能（两问都要求用题中给出的物理量表示）。

一个氘核和一个氚核结合成氦时，释放的核能为ΔE，阿伏加德罗常数为N_A,则4克氘核与6克氚核完全反应，发生的质量亏损是

A．2NAΔEc^2

B．4NAΔEc^2

C．

D．