云室处在磁感应强度为B的匀强磁场中,一静止的质量为M的原子核在云室中发生一次 衰变。
衰变。 粒子的质量为m,带电量为q,其运动轨迹在与磁场垂直的平面内。现测得
粒子的质量为m,带电量为q,其运动轨迹在与磁场垂直的平面内。现测得 粒子运动的迹道半径为R,试求在衰变过程中的质量亏损(涉及动量问题时,亏损的质量可忽略不计)。
粒子运动的迹道半径为R,试求在衰变过程中的质量亏损(涉及动量问题时,亏损的质量可忽略不计)。
在真空中,原来静止的原子核 在进行
在进行 衰变,放出
衰变,放出 粒子的动能为E0,假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计。
粒子的动能为E0,假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计。
①写出衰变的核反应方程;
②求衰变过程中总的质量亏损。
我国科学家研制世界上第一个全超导核聚变“人造太阳”,用来解决人类的能源之需,代替煤、石油等不可再生资源.“人造太阳”的实验装置模拟太阳产生能量的方式.从海水中提取氘和氚,使其在上亿度的高温下产生聚变反应,反应方程式为: .设氘(
.设氘( )的质量为m1,氚(
)的质量为m1,氚( )的质量为m2,氦(
)的质量为m2,氦( )的质量为m3,中子(
)的质量为m3,中子( )的质量为m4,c为光在真空中传播的速度.核反应放出的能量E为
)的质量为m4,c为光在真空中传播的速度.核反应放出的能量E为
A. |
B. |
C. |
D. |
太阳因核聚变释放出巨大的能量,同时其质量不断减少.太阳每秒钟辐射出的能量约为4×1026 J,根据爱因斯坦质能方程,太阳每秒钟减少的质量最接近( )
| A.1036 kg | B.1018 kg |
| C.1013 kg | D.109 kg |
1932年,英国物理学家查德威克用α射线轰击铍核(Be)时,产生了碳核( C)和一种不受电场和磁场影响、穿透能力很强的射线,经过进一步证实,这种射线是( )
C)和一种不受电场和磁场影响、穿透能力很强的射线,经过进一步证实,这种射线是( )
A.光子流 B.中子流
C.电子流 D.质子流
云室处在磁感应强度为B的匀强磁场中,一静止的质量为M的原子核在云室中发生一次α衰变,α粒子的质量为m,电荷量为q,其运动轨迹在与磁场垂直的平面内,且轨道半径为R,试求衰变过程中的质量亏损.(注:涉及动量问题时,亏损的质量可忽略不计)
为确定爱因斯坦的质能方程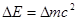 的正确性,设计了如下实验:用动能为
的正确性,设计了如下实验:用动能为 0MeV的质子轰击静止的锂核
0MeV的质子轰击静止的锂核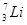 ,生成两个
,生成两个 粒子,测得两个
粒子,测得两个 粒子的动能之和为
粒子的动能之和为 MeV,已知质子、
MeV,已知质子、 粒子、锂粒子的质量分别取
粒子、锂粒子的质量分别取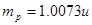 、
、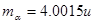 、
、 ,求:
,求:
①写出该反应方程.
②通过计算说明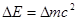 正确.(1u = 1.6606×10-27㎏)
正确.(1u = 1.6606×10-27㎏)
太阳在不断地向外辐射能量,因而其质量也在不断地减少.若太阳每秒钟辐射的总能量为4×1026 J,试计算太阳在1 s内失去的质量,估算5000年内其质量总共减小了多少,并与太阳的总质量2×1027 t比较之.
(1)用质子轰击锂核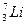 生成2个α粒子.己知质子质量mp=1.0078u,α粒子的质量ma="4.0026" u,锂核质量mLi="7.0160" u,已知 lu的质量对应的能量为931.5MeV。
生成2个α粒子.己知质子质量mp=1.0078u,α粒子的质量ma="4.0026" u,锂核质量mLi="7.0160" u,已知 lu的质量对应的能量为931.5MeV。
写出该反应的核反应方程式 ,核反应中释放出的能量为 。
(2)如图甲所示,在光滑水平面上的两小球发生正碰.小球的质量分别为m1和m2.图乙为它们碰撞后的s-t 图象.已知m1=0.1 kg.求m2的质量。
已知氘核质量为2.0136u,中子质量为1.0087u,
 He核的质量为3.0150u。
He核的质量为3.0150u。
⑴写出两个氘核聚变成 He的核反应方程;
He的核反应方程;
⑵计算上述核反应中释放的核能 ;
;
⑶若两氘核以相等的动能0.35MeV做对心碰撞即可发生上述核反应,且释放的核能全部转化为机械能,则反应中生成的  He核和中子的动能各是多少?
He核和中子的动能各是多少?
氘核、氚核、中子、氦核的质量分别是 、
、 、
、 和
和 ,如果氘核和氚核结合生成氦核,则下列说法中正确的是
,如果氘核和氚核结合生成氦核,则下列说法中正确的是
A.核反应方程式为 |
| B.这是一个裂变反应 |
C.核反应过程中的质量亏损 |
D.核反应过程中释放的核能 |
设宇宙射线粒子的能量是其静止能量的k倍.则粒子运动时的质量等于其静止质量的倍,粒子运动速度是光速的倍。
一个氢原子的质量为1.6736×10-27kg,一个锂原子的质量为11.6505×10-27kg,一个氦原子的质量为6.6467×10-27kg。一个锂核受到一个质子轰击变为2个α粒子,⑴写出核反应方程,并计算该反应释放的核能是多少?⑵1mg锂原子发生这样的反应共释放多少核能?