在真空中,原来静止的原子核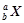 在进行
在进行 衰变,放出
衰变,放出 粒子的动能为E0,假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计。
粒子的动能为E0,假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计。
①写出衰变的核反应方程;
②求衰变过程中总的质量亏损。
在真空中,原来静止的原子核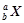 在进行
在进行 衰变,放出
衰变,放出 粒子的动能为E0,假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计。
粒子的动能为E0,假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计。
①写出衰变的核反应方程;
②求衰变过程中总的质量亏损。