当物体做匀加速直线运动时，则 ）
| A．在任何相等时间内的位移都相等; |
| B．在任意两个连续相等时间内的位移差都相等; |
| C．第1秒内、第2秒内和第3秒内的位移之比为1:3:5; |
| D．速度和时间不一定成正比 |
如图甲所示，电荷量为q=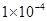
C的带正电的小物块置于绝缘水平面上，所在空间存在方向沿水平向右的电场，电场强度E的大小与时间的关键如图乙所示，物块运动速度与时间t的关系如图丙所示，取重力加速度
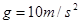，求：
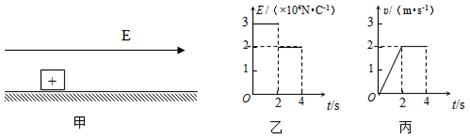
（1）前2s内电场力做的功；
（2）物块的质量；
（3）物块与水平面的动摩擦因数。
一劲度系数k="800" N/m的轻质弹簧两端分别连接着质量均为12 kg的物体A、B，将它们竖直静止放在水平面上，如图所示。现将一竖直向上的变力F作用在A上，使A开始向上做匀加速运动，经0.40 s物体B刚要离开地面，取g ="10" m/s2，试求这0.40s内力F所做的功。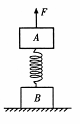
为了测量某住宅大楼每层的平均高度（层高）及电梯运行情况，甲、乙两位同学在一楼 电梯内用电子体重计及秒表进行了以下实验，甲同学站在体重计上，乙同学记录电梯从地面一楼到顶层全过程中，体重计示数随时间变化的情况，并作出了如图所示的图象．已知t=0时，电梯静止不动，从电梯内楼层按钮上获知该大楼共19层．求：
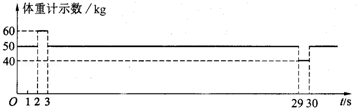
（1）电梯启动和制动时的加速度大小；
（2）该大楼的层高．
历史上有些科学家曾把在相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”（现称“另类匀变速直线运动”），“另类加速度”定义为 A = 
，其中v0 和vt 分别表示某段位移 s 内的初速度和末速度。A > 0表示物体做加速运动，A < 0表示物体做减速运动。而现在物理学中加速度的定义式为 a =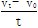 
，下列说法正确的是：
| A．若A不变，则 a 也不变。 |
| B．若A > 0且保持不变，则 a 逐渐变小。 |
C．若A不变，则物体在中间位置处的速度为  。 |
D．若A不变，则物体在中间位置处的速度为  |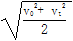
一物块质量m=1kg静止置于光滑水平面上，受到一个如图所示的力F的作用在水平面内运动，力F是一个周期性变化的力，规定向东为力F的正方向，求：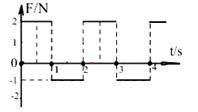
（1）第1s内和第2s内的加速度大小；
（2）t=8.5s时物块离开出发点的位移大小。
如图所示为甲、乙两物体沿同一直线运动的s-t图像，下列说法中正确的是( )
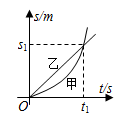
| A．两物体的初速度都为零 |
| B．甲、乙两物体相遇时，速度大小相等 |
| C．甲物体做变加速直线运动，乙物体做匀加速直线运动 |
| D．在t1时间内两物体的平均速度大小相等 |
如图，A、B分别是甲、乙两小球从同一地点沿同一直线运动的v﹣t图象，根据图象可以判断（ ）
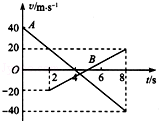
A．两球在t=2s时速率相等
B．两球在t=8s时相距最远
C．两球运动过程中不会相遇
D．甲、乙两球做初速度方向相反的匀减速直线运动，加速度大小相同方向相反
一列货车以10m/s的速度在铁路上匀速行驶，由于调度事故，在大雾中后面600处有一列快车以20m/s的速度在同一轨道上行驶，快车司机赶快合上制动器，快车要滑行2000才能停下来，请判断两车会不会相撞？
跳伞运动员从350m的高空离开直升机，自由下落一段距离后才打开降落伞，设开伞后以2 m/s2的加速度匀减速下降，到达地面的速度为4 m/s，求他下落的总时间及自由下落的距离．(g取10 m/s2)
如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量相等，均为m，弹簧的劲度系数为k，C为一固定挡板。系统处于静止状态．现开始用沿斜面方向的力F（F未知）拉物块A使之向上做加速度为a的匀加速运动，当物块B刚要离开C时，沿斜面方向的力F（F未知）保持此时的值变为恒力，且此时弹簧与物块A连接处断裂，物块A在恒力作用下继续沿斜面向上运动．重力加速度为g，求：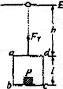
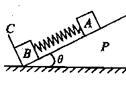
（1）恒力F的大小；
（2）物块A从断裂处继续前进相同的距离后的速度．
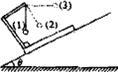
如图一可视为质点的物体，在倾角θ=30°的固定斜面上，向下轻轻一推，它恰好匀速下滑．已知斜面长度为L=5m．求：欲使物体由斜面底端开始，沿斜面冲到顶端，物体上滑时的初速度至少为多大？（g取10m/s2）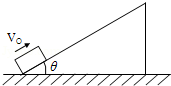
如图所示，A和B是两个相同的带电小球，可视为质点，质量均为m，电荷量均为q，A固定在绝缘地面上，B放在它的正上方很远距离的一块绝缘板上，现手持绝缘板使B从静止起以恒定的加速度a（a＜g）竖直下落h时，B与绝缘板脱离．静电力常量为k，求：
（1）B刚脱离绝缘板时的动能．
（2）B在脱离绝缘板前的运动过程中，电场力和板的支持力对B做功的代数和W．
（3）B脱离绝缘板时离A的高度H．
行驶了全程的一半，然后匀减速行驶了后一半，到终点时恰好停止，则全程的平均速度为（ ）
粤公网安备 44130202000953号