高中物理放射性同位素的应用试题

(8分)如图所示，一质量为8m的长木板静止在光滑水平面上，某时刻一质量为m的小铁块以速度从木板的右端滑上木板．已知铁块与木板间的动摩擦因数为，重力加速度大小为g，木板足够长，求：

(1)铁块与木板的加速度大小；
(2)当木板在水平面上加速滑行的距离为x时，铁块在木板上滑行的长度为多少?

当物体做匀加速直线运动时，则    ）

A．在任何相等时间内的位移都相等;

B．在任意两个连续相等时间内的位移差都相等;

C．第1秒内、第2秒内和第3秒内的位移之比为1:3:5;

D．速度和时间不一定成正比

在民航业内，一直有“黑色10分钟”的说法，即从全球已发生的飞机事故统计数据来看，大多数的航班事故发生在飞机起飞阶段的3分钟和着陆阶段的7分钟。飞机安全事故虽然可怕，但只要沉着冷静，充分利用逃生设备，逃生成功概率相当高，飞机失事后的90秒内是逃生的黄金时间。如图为飞机逃生用的充气滑梯，滑梯可视为理想斜面，已知斜面长L=8m，斜面倾斜角θ=37°，人下滑时与充气滑梯间动摩擦因素为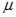=0.5。不计空气阻力，g=10m/s²，Sin37°=0.6，cos37°=0.8， 求：

（1）旅客从静止开始由滑梯顶端滑到底端逃生，需要多长时间？
（2）一旅客若以V₀=4.0m/s的初速度抱头从舱门处水平逃生，当他落到充气滑梯上后没有反弹，由于有能量损失，结果他以v=4.0m/s的速度开始沿着滑梯加速下滑。该旅客以这种方式逃生与（1）问中逃生方式相比，节约了多长时间？

如图甲所示，静止在水平面C上足够长的木板B左端放着小物块A。某时刻，A受到水平向右的外力F作用，F随时间t的变化规律如图乙所示。A、B间最大静摩擦力大于B、C之间的最大静摩擦力，假设最大静摩擦力等于滑动摩擦力。则在拉力逐渐增大的过程中，下列反映A、B运动过程中的加速度及A与B间摩擦力f₁、B与C间摩擦力f₂随时间变化的图线中正确的是（     ）

有一平板车，车厢底板光滑，车厢的前后端均有挡板，前后挡板间的距离L=10m。将一个小物体放在底板上并靠着后挡板，让平板车在平直轨道上由静止开始做匀加速直线运动，加速度a₁=2m/s²。经时间t₁= 4s，平板车开始刹车，平板车立即开始做匀减速直线运动，加速度大小a₂=4m/s²，求：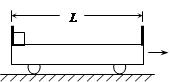

(1)平板车刚开始刹车时的速度v
(2)平板车从开始运动到停止运动通过的位移x
(3)从平板车开始刹车至小物体撞到平板车的前挡板经历的时间t

如图所示为甲、乙沿同一直线运动的速度图象，由图象可知错误的是

A．甲做匀减速直线运动，加速度为

B．乙做匀加速直线运动，加速度为4

C．运动到甲、乙速度相同时，甲、乙的位移均为50m

D．甲、乙沿同向运动，乙开始运动时间比甲晚5s

如图（甲）所示，质量为M的木板静止在光滑水平地面上，现有一质量为m的滑块以一定的初速度v₀从木板左端开始向右滑行．两者的速度大小随时间变化的情况如图（乙）所示，则由图可以断定（   ）

A．滑块与木板间始终存在相对运动

B．滑块未能滑出木板

C．滑块质量大于木板质量

D．在t1时刻滑块从木板上滑出

如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量相等，均为m，弹簧的劲度系数为k，C为一固定挡板。系统处于静止状态．现开始用沿斜面方向的力F（F未知）拉物块A使之向上做加速度为a的匀加速运动，当物块B刚要离开C时，沿斜面方向的力F（F未知）保持此时的值变为恒力，且此时弹簧与物块A连接处断裂，物块A在恒力作用下继续沿斜面向上运动．重力加速度为g，求：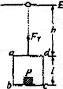



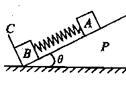
（1）恒力F的大小；
（2）物块A从断裂处继续前进相同的距离后的速度．

如图一可视为质点的物体，在倾角θ=30°的固定斜面上，向下轻轻一推，它恰好匀速下滑．已知斜面长度为L=5m．求：欲使物体由斜面底端开始，沿斜面冲到顶端，物体上滑时的初速度至少为多大？（g取10m/s²）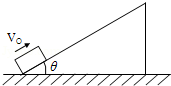

一辆汽车以速度行驶了全程的一半，然后匀减速行驶了后一半，到终点时恰好停止，则全程的平均速度为（  ）

A．

B．

C．

D．

如图所示，A和B是两个相同的带电小球，可视为质点，质量均为m，电荷量均为q，A固定在绝缘地面上，B放在它的正上方很远距离的一块绝缘板上，现手持绝缘板使B从静止起以恒定的加速度a（a＜g）竖直下落h时，B与绝缘板脱离．静电力常量为k，求：

（1）B刚脱离绝缘板时的动能．
（2）B在脱离绝缘板前的运动过程中，电场力和板的支持力对B做功的代数和W．
（3）B脱离绝缘板时离A的高度H．

一列列车长100m，以v₁=30m/s的速度正常行驶，当通过1 000m长的大桥时，必须以v₂=20m/s的速度行驶．在列车上桥前需提前减速，当列车头刚上桥时速度恰好为20m/s，列车全部离开大桥时又需通过加速恢复原来的速度．减速过程中，加速度大小为0.25m/s²．加速过程中，加速度大小为1m/s²，则该列车从减速开始算起，到过桥后速度达到30m/s，共用了多长时间？

一物体沿一直线从静止开始运动且同时开始计时，其加速度随时间周期性变化的关系图线（a﹣t图）如图所示，求：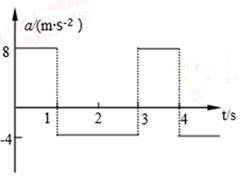

（1）物体在第4s末的速度；
（2）物体在前3s内的位移；
（3）物体在第4s内的位移．

质量为m=1kg的物体以初速V₀=12m/s竖直上抛，空气阻力大小为其重力的0.2倍，g取10m/s²，求：
（1）该物体上升和下降时的加速度之比；
（2）求整个过程中物体克服阻力做功的平均功率P₁和物体落回抛出点时重力的瞬时功率P₂。

三角传送带以1m/s的速度逆时针匀速转动，两边的传送带长都是2m，且与水平方向的夹角均为37°。现有两小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑，物块与传送带间的动摩擦因数均为0．5，下列说法正确的是（  ）

A．物块A先到达传送带底端
B．物块A、B同时到达传送带底端
C．传送带对物块A、B均做负功
D．物块A、B在传送带上的划痕长度不相同