拥堵已成为现代都市一大通病,发展“空中轨道列车”(简称空轨)是缓解交通压力重要举措。如图所示,它是一种悬挂式单轨交通系统,不仅施工简单、快捷,造价也仅为地铁造价的六分之一左右,下表是有关空轨列车的部分参数。假如多辆空轨列车在同一轨道上同向行驶,为了安全,前后车之间应保持必要的距离,假设前方车辆突然停止,后车司机从发现这一情况,经操纵刹车,到汽车开始减速所经历的时间(即反应时间)t=0.50s,求空轨列车的安全车距应至少设定为多少?(g=10m/s2)
| 行车速度 |
约13 m/s |
车辆起动加速度 |
1.0 m/s2 |
| 车辆高度 |
2623 mm |
紧急制动加速度 |
6.50 m/s2 |
| 车辆宽度 |
2244 mm |
车辆净重 |
8455 kg |
| 平面转弯半径 |
≥30 m |
车辆满载重 |
15000kg |
猎豹是目前世界上在陆地奔跑速度最快的动物,时速可达110多公里,但不能维持长时间高速奔跑,否则会因身体过热而危及生命。猎豹在一次追击猎物时(如图),经4s速度由静止达到最大,然后匀速运动保持了4s仍没追上猎物,为保护自己它放弃了这次行动,以3m/s2的加速度减速,经10s停下,设此次追捕猎豹始终沿直线运动.求:
(1)猎豹加速时的平均加速度.
(2)猎豹奔跑的最大速度.
如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5kg的物体,它与传送带间的动摩擦因数μ=0.5,已知传送带从A→B的长度L=16m,则物体从A到B需要的时间为多少? 
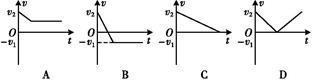
某物体沿一直线运动,其v-t图象如图所示,则下列说法中正确的是( )
| A.第2s内和第3s内的速度方向相反 |
| B.第2s内和第3s内的加速度方向相反 |
| C.第3s内速度方向与加速度方向相反 |
| D.第5s内速度方向与加速度方向相反 |
一汽车从静止开始做匀加速直线运动,然后刹车做匀减速直线运动,直到停止.下列速度v和位移x的关系图像中,能描述该过程的是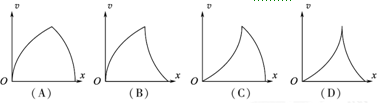
(多选)如图所示,绷紧的水平传送带始终以恒定速率v1运行.初速度大小为v2的小物块从与传送带等高的光滑水平地面上滑上传送带,以地面为参考系,v2>v1.从小物块滑上传送带开始计时,其v t图象可能的是( )
t图象可能的是( )
如图所示,x轴与水平传送带重合,坐标原点O在传送带的左端,传送带长L=8 m,匀速运动的速度v0=5 m/s。一质量m=1 kg的小物块轻轻放在传送带上xP=2 m的P点,小物块随传送带运动到Q点后恰好能冲上光滑圆弧轨道的最高点N点。小物块与传送带间的动摩擦因数μ=0.5,重力加速度g=10 m/s2。求:
(1)N点的纵坐标;
(2)小物块在传送带上运动产生的热量;
(3)若将小物块轻放在传送带上的某些位置,小物块均能沿光滑圆弧轨道运动(小物块始终在圆弧轨道运动不脱轨)到达纵坐标yM=0.25 m的M点,求这些位置的横坐标范围。
汽车刹车后开始做匀减速运动,第1s内和第2s内的位移分别为3m和2m,那么从2s末开始,汽车还能继续向前滑行的最大距离是 ( )
| A.1.5m | B.1.25m | C.1.125m | D.1m |
如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B,它们的质量相等,均为m,弹簧的劲度系数为k,C为一固定挡板。系统处于静止状态.现开始用沿斜面方向的力F(F未知)拉物块A使之向上做加速度为a的匀加速运动,当物块B刚要离开C时,沿斜面方向的力F(F未知)保持此时的值变为恒力,且此时弹簧与物块A连接处断裂,物块A在恒力作用下继续沿斜面向上运动.重力加速度为g,求: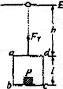
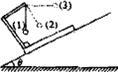
(1)恒力F的大小;
(2)物块A从断裂处继续前进相同的距离后的速度.
如图一可视为质点的物体,在倾角θ=30°的固定斜面上,向下轻轻一推,它恰好匀速下滑.已知斜面长度为L=5m.求:欲使物体由斜面底端开始,沿斜面冲到顶端,物体上滑时的初速度至少为多大?(g取10m/s2)
如图所示,A和B是两个相同的带电小球,可视为质点,质量均为m,电荷量均为q,A固定在绝缘地面上,B放在它的正上方很远距离的一块绝缘板上,现手持绝缘板使B从静止起以恒定的加速度a(a<g)竖直下落h时,B与绝缘板脱离.静电力常量为k,求:
(1)B刚脱离绝缘板时的动能.
(2)B在脱离绝缘板前的运动过程中,电场力和板的支持力对B做功的代数和W.
(3)B脱离绝缘板时离A的高度H.
一列列车长100m,以v1=30m/s的速度正常行驶,当通过1 000m长的大桥时,必须以v2=20m/s的速度行驶.在列车上桥前需提前减速,当列车头刚上桥时速度恰好为20m/s,列车全部离开大桥时又需通过加速恢复原来的速度.减速过程中,加速度大小为0.25m/s2.加速过程中,加速度大小为1m/s2,则该列车从减速开始算起,到过桥后速度达到30m/s,共用了多长时间?
一物体沿一直线从静止开始运动且同时开始计时,其加速度随时间周期性变化的关系图线(a﹣t图)如图所示,求: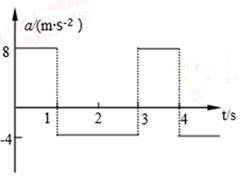
(1)物体在第4s末的速度;
(2)物体在前3s内的位移;
(3)物体在第4s内的位移.
质量为m=1kg的物体以初速V0=12m/s竖直上抛,空气阻力大小为其重力的0.2倍,g取10m/s2,求:
(1)该物体上升和下降时的加速度之比;
(2)求整个过程中物体克服阻力做功的平均功率P1和物体落回抛出点时重力的瞬时功率P2。