一质点沿坐标轴Ox做变速直线运动,它在坐标轴上的坐标x随时间t的变化关系为x=5+2t3,速度v随时间t的变化关系为v=6t2,其中v、x和t的单位分别是m/s、m和s。设该质点在t=0到t=1s内运动位移为s和平均速度为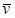 ,则
,则
A.s="6m" ,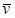 =6m/s =6m/s |
B.s="2m" ,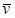 ="2m/" s ="2m/" s |
C.s="7m" ,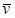 =7m/s =7m/s |
D.s="3m" ,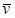 =3m/s =3m/s |
现在的物理学中加速度的定义式为 ,而历史上有些科学家曾把相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”定义为
,而历史上有些科学家曾把相等位移内速度变化相等的单向直线运动称为“匀变速直线运动”(现称“另类匀变速直线运动”),“另类加速度”定义为 ,其中v0和vt分别表示某段位移s内的初速度和末速度。A>0表示物体做加速运动,A<0表示物体做减速运动。则下列说法正确的是
,其中v0和vt分别表示某段位移s内的初速度和末速度。A>0表示物体做加速运动,A<0表示物体做减速运动。则下列说法正确的是
| A.若A不变,则a也不变 |
B.若A不变,则物体在位移中点处的速度比  大 大 |
C.若a 不变,则物体在中间时刻的速度为  |
| D.若a>0且保持不变,则A逐渐变小 |
一个做匀变速直线运动的物体,其位移和时间的关系是X=18t-6t2,则它的速度为零的时刻是:
| A.6S; | B.3S; |
| C.1.5S; | D.18S; |
物体作匀加速直线运动,已知加速度为2m/s2,那么 ()
| A.任意1秒时间内物体的末速度一定等于初速度的2倍 |
| B.任意1秒时间内物体的末速度一定比初速度大2m/s |
| C.第5s的初速度一定比第4s的末速度大2m/s |
| D.第5s的末速度一定比第4s的初速度大2m/s |
由静止开始做匀加速直线运动的汽车,第1s内通过0.4m位移,求:
(1)汽车在第1s末的速度为多大?(2)汽车在第2s内通过的位移为多大?
甲、乙两车在同一平直公路上由A站驶向B站.它们同时由静止从A站出发,最后都到达B站停下.行驶过程中,甲车先做匀加速运动,后做匀减速运动;乙车先做匀加速运动,再做匀速运动,最后做匀减速运动.若两车在加速和减速中的加速度大小相等,则
| A.甲车先到达B站 |
| B.乙车先到达B站 |
| C.在行驶过程中甲车的最大速度大于乙车的最大速度 |
| D.在行驶过程中乙车的最大速度大于甲车的最大速度 |
某物体运动的v-t图象如图所示,则下列说法正确的是( )
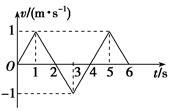
| A.物体在第2 s内和第3 s内的加速度是相同的 |
| B.物体在第1 s 末运动方向发生改变 |
| C.物体在第6 s末返回出发点 |
| D.物体在第5 s末离出发点最远,且最大位移为0.5 m |
如右图所示,静止的倾斜传送带上有一木块正在匀速下滑,当传送带突然顺时针转动后,下列说法正确的是( )
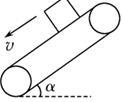
| A.木块所受摩擦力变大 | B.木块到底部所走位移变大 |
| C.木块到底部所用时间变长 | D.木块到底部所用的时间不变 |
甲乙两辆汽车在平直的公路上沿同一方向作直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v﹣t图中(如图),直线a、b分别描述了甲乙两车在0~20秒的运动情况.关于两车之间的位置关系,下列说法正确的是( )

| A.在0~10秒内两车逐渐靠近 |
| B.在10~20秒内两车逐渐远离 |
| C.在5~15秒内两车的位移相等 |
| D.在t=10秒时两车在公路上相遇 |
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是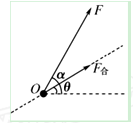
A.加速时加速度的大小为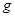 |
B.加速时动力的大小等于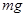 |
C.减速时动力的大小等于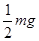 |
| D.减速飞行时间t后速度为零 |
如图甲、乙所示,为同一打点计时器打出的两条纸带,由纸带可知( )

| A.在打下计数点“0”至“5”的过程中,纸带甲的平均速度比乙的大 |
| B.在打下计数点“0”至“5”的过程中,纸带甲的平均速度比乙的小 |
| C.纸带甲的加速度比乙的大 |
| D.纸带甲的加速度比乙的小 |
一辆汽车在平直公路上做刹车实验,若从t=0时刻起汽车在运动过程的位移x与速度的平方v2的关系如图所示,下列说法正确的是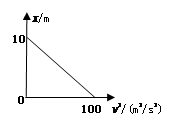
| A.刹车过程汽车加速度大小为10m/s2 |
| B.刹车过程持续的时间为5s |
| C.刹车过程经过3s的位移为7.5m |
| D.t=0时刻的初速度为l0m/s |
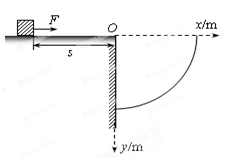
据《每日邮报》2015年4月27日报道,英国威尔士一只100岁的宠物龟“T夫人”(Mrs T)在冬眠的时候被老鼠咬掉了两只前腿。“T夫人”的主人为它装上了一对从飞机模型上拆下来的轮胎。现在它不仅又能走路,甚至还能“跑步”了,现在的速度比原来快一倍。如图所示,设“T夫人”质量m=1.0kg在粗糙水平台阶上静止,它与水平台阶表面的阻力简化为与体重的k倍,k=0.25,且与台阶边缘O点的距离s=5m。在台阶右侧固定了一个1/4圆弧挡板,圆弧半径R=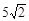 m,今以O点为原点建立平面直角坐标系。“T夫人”通过后腿蹬地可提供F=5N的水平恒力,已知重力加速度
m,今以O点为原点建立平面直角坐标系。“T夫人”通过后腿蹬地可提供F=5N的水平恒力,已知重力加速度 。
。
(1)“T夫人”为了恰好能停在O点,蹬地总距离为多少?
(2)“T夫人”为了恰好能停在O点,求运动最短时间;
(3)若“T夫人”在水平台阶上运动时,持续蹬地,过O点时停止蹬地,求“T夫人” 击中挡板上的位置的坐标。