高中物理波长、频率和波速的关系试题

有两列简谐横波、在同一媒质中沿轴正方向传播，波速均为。在时，两列波的波峰正好在处重合，如图所示。
（1）求两列波的周期和。

（2）求时，两列波的波峰重合处的所有位置。

（3）辨析题：分析并判断在时是否存在两列波的波谷重合处。某同学分析如下：既然两列波的波峰存在重合处，那么波谷与波谷重合处也一定存在。只要找到这两列波半波长的最小公倍数，……，即可得到波谷与波谷重合处的所有位置。

你认为该同学的分析正确吗？若正确，求出这些点的位置。若不正确，指出错误处并通过计算说明理由。

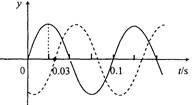
一列简谐横波沿直线传播，该直线上的、两点相距4.42 。图中实、虚两条曲线分别表示平衡位置在、两点处质点的振动曲线。从图示可知（）

A．	此列波的频率一定是10
B．	此列波的波长一定是0.1
C．	此列波的传播速度可能是34
D．	点一定比 点距波源近

如图甲所示，均匀介质中，各质点的平衡位置在同一直线上（图中只画出前13个质点），相邻两质点间的距离相等.计时开始时质点1由平衡位置向上振动，经过6 s，前13个质点第一次形成如图乙所示的波形.再过3 s，这13个质点所形成波的形状为下图中的（   ）

一列沿x轴正方向传播的简谐横波，t=0时刻的波形如图中实线所示，t="0.2" s时刻的波形如图中的虚线所示，则（   ）

A．质点P的运动方向向右

B．波的周期可能为0.27 s

C．波的频率可能为1.25 Hz

D．波的传播速度可能为20 m/s