高中物理横波的图象综合题

（1）下列说法中正确的是 （     ）

A．交通警通过发射超声波测量车速，利用了波的干涉原理

B．电磁波的频率越高，它所能携带的信息量就越大，所以激光可以比无线电波传递更多的信息

C．单缝衍射中，缝越宽，条纹越亮，衍射现象也越明显

D．地面上测得静止的直杆长为L，则在沿杆方向高速飞行火箭中的人测得杆长应小于L

（2）一列简谐横波在t=0时刻的波形如图所示，质点P此时刻沿-y运动，经过0.1s第一次到达平衡位置，波速为5m/s，那么

①该波沿       （选填“+x”或“-x”）方向传播；
②图中Q点（坐标为x=7.5m的点）的振动方程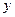=" "      cm；
③P点的横坐标为x=      m.

图10．3－8是一列简谐波在某一时刻的波的图象，虚线是0.2s后的波的图象，求这列波可能的速度．

一列沿x轴传播的横波在某一时刻的波形图象如图12-2-12所示，已知波的传播速率是16 m/s，且该时刻P质点沿y轴正方向运动。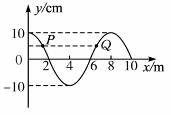

图12-2-12
(1)指出这列波的传播方向。
(2)图示时刻Q质点与P质点的位移相同，那么下一时刻它们的位移还相等吗？Q点的速度将如何变化？
(3)画出再经过0.125 s时的波形图象。

如图10.3－2是某一列简谐波在t＝3.0s时的波形图象，已知这列波波速v=1.5m/s，向x轴正方向传播，要求作出t＝3.2s时的波的图象．

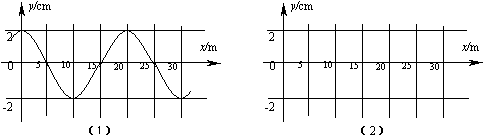
一列简谐波在x轴上传播，波速为50m/s． 已知 t＝0时刻的波动图象如图 (1)所示，图中x=5m处的质点此时正经过平衡位置沿 y轴的正方向运动．将t＝0.5s时的波动图象画在图(2)上(至少要画出一个波长)．

在波的传播方向上有两个质点P和Q，它们的平衡位置相距s="1.2" m,且大于一个波长，介质中的波速v="2" m/s,P和Q的振动图线如图12-2-14所示，求振动周期的最大值，并画出t=0时的波的图象.

图12-2-14

如图为一简谐波在时，对应的波形图，介质中的质点P做简谐运动的表达式为，求该波的速度，并指出时的波形图(至少画出一个波长)

如图所示为一列简谐横波在某一时刻的波形图象，已知波速v＝40cm/s，求：
(1)这列波的周期是多少？
(2)在图中标出A，B，C，D各点的运动方向．
(3)在图中作出0.125s后的波形图象．

如图所示，S是波源，振动频率f=100Hz，产生的简谐波向右传播，波速v=80m／s，波传播过程中经过P、Q两点，已知距离SP＝4.2m，SQ＝5.4m。

在某一时刻t，当S点通过平衡位置向上运动时，P点和Q点处于波峰，还是处于波谷，或者处于其他位置?

一简谐横波在时刻t=0时的波形图象所示，传播方向自左向右，已知t₂=0.6s末，A点出现第三次波峰。试求：

（1）该简谐波的周期；
（2）该简谐波传播到B点所需的时间；
（3）B点第一次出现波峰时，A点经过的路程。

一列简谐波在x轴上传播，波速为50 m/s，已知t₀=0时刻如图12-2-12所示，图中M处的质点此时正经过平衡位置沿y轴正方向运动，将t="0.5" s时的波形图画在图12-2-12上，用②标出.（至少画出一个波长）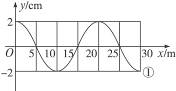

图12-2-12

（1）由波源S形成的简谐横波在均匀介质中向左、右传播。波源振动的频率为20 Hz，波速为16 m/s。已知介质中P、Q两质点位于波源S的两侧，且P、Q和S的平衡位置在一条直线上，P、Q的平衡位置到S的平衡位置之间的距离分别为15．8 m、14．6 m，P、Q开始震动后，下列判断正确的是_____。

A．	P、Q两质点运动的方向始终相同
B．	P、Q两质点运动的方向始终相反
C．	当S恰好通过平衡位置时，P、Q两点也正好通过平衡位置
D．	当S恰好通过平衡位置向上运动时，P在波峰
E．	当S恰好通过平衡位置向下运动时，Q在波峰

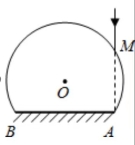
（2）如图，玻璃球冠的折射率为 $\sqrt{3}$ ，其底面镀银，底面的半径是球半径的 $\frac{\sqrt{3}}{2}$ 倍；在过球心O且垂直于底面的平面（纸面）内，有一与底面垂直的光线射到玻璃球冠上的M点，该光线的延长线恰好过底面边缘上的A点。求该光线从球面射出的方向相对于其初始入射方向的偏角。

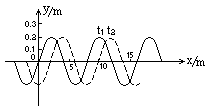
一列横波在x轴线上传播着，在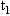=0和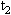=0.005s时的波形曲线如图所示。
(1)由图中读出波的振幅和波长。
(2)设周期大于(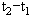)。如果波向右传播，波速多大?如果波向左传播，波速又是多大?
(3)设周期小于(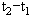)并且波速为6000m/s，求波的传播方向。

（1）P、Q是一列简谐横波中的质点，相距30m，各自的振动图象如图所示．

①此列波的频率f＝________Hz. ②如果P比Q离波源近，且P与Q间距离小于1个波长，那么波长λ＝________m.
③如果P比Q离波源远，那么波长λ＝________m.
（2）如图所示，半圆形玻璃砖的半径为R，光屏PQ置于直径的右端并与直径垂直，一复色光与竖直方向成α＝30°角射入玻璃砖的圆心，由于色光中含有两种单色光，故在光屏上出现了两个光斑，玻璃对两种单色光的折射率分别为n₁＝和n₂＝，求：
①这两个光斑之间的距离；
②为使光屏上的光斑消失，复色光的
入射角至少为多少

如图所示为波源O振动1.5s时沿波的传播方向上部分质点振动的波形图，已知波源O在t=0时开始沿x轴负方向振动，t=1.5s时它正好第二次到达波谷，问：

（1）y=5.4m的质点何时第一次到达波峰？
（2）从t=0开始至y=5.4m的质点第一次到达波峰的这段时间内，波源通过的路程是多少？