如图所示,四条水平虚线等间距地分布在同一竖直面上,间距为h.在Ⅰ、Ⅱ两区间分布着完全相同、方向水平向里的磁场,磁感应强度大小按B-t图变化(图中B0已知).现有一个长方形金属线框ABCD,质量为m,电阻为R,AB=CD=L,AD=BC=2h.用一轻质细线把线框ABCD竖直悬挂着,AB边恰好在Ⅰ区的正中央.t0(未知)时刻细线恰好松弛,之后立即剪断细线,当CD边到达M3N3时线框恰好匀速运动.(空气阻力不计,g=10m/s2)求: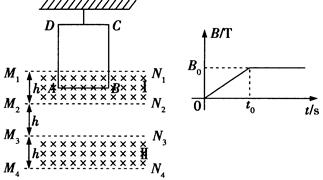
(1)t0的值;
(2)线框AB边到达M2N2时的速率v;
(3)从剪断细线到整个线框通过两个磁场区的过程中产生的电能有多少?
如图所示间距为L的光滑平行金属导轨,水平放置在竖直方向的磁感应强度为B的匀强磁场中,一端接阻值是R的电阻。一电阻为R0、质量为m的导体棒放置在导轨上,在外力作用下从 的时刻开始运动,其速度随时间的变化规律
的时刻开始运动,其速度随时间的变化规律 ,不计导轨电阻。则从
,不计导轨电阻。则从 到
到 时间内外力F所做的功为( )
时间内外力F所做的功为( )
A
 B.
B.  C.
C. 
 D.
D.
如图,竖直平面内放着两根间距L = 1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R= 2Ω的电阻,N板上有一小孔Q,在金属板M、N及CD上方有垂直纸面向里的磁感应强度B0= 1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T。有一质量M = 0.2kg、电阻r =1Ω的金属棒搭在MN之间并与MN良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点静止释放一个比荷 的正离子,经电场加速后,以v =200m/s的速度从Q点垂直于N板边界射入右侧区域。不计离子重力,忽略电流产生的磁场,取g=
的正离子,经电场加速后,以v =200m/s的速度从Q点垂直于N板边界射入右侧区域。不计离子重力,忽略电流产生的磁场,取g= 。求:
。求:
(1)金属棒达最大速度时,电阻R两端电压U;
(2)电动机的输出功率P;
(3)离子从Q点进入右侧磁场后恰好不会回到N板,Q点距分界线高h等于多少。
如图所示,凸字形硬质金属线框质量为
,相邻各边互相垂直,且处于同一竖直平面内,
边长为
,
边长为
,
与
平行,间距为
。匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面。开始时,
边到磁场上边界的距离为
,线框由静止释放,从
边进入磁场直到
、
边进入磁场前,线框做匀速运动,在
、
边离开磁场后,
边离开磁场之前,线框又做匀速运动。线框完全穿过磁场过程中产生的热量为
。线框在下落过程中始终处于原竖直平面内,且
.
边保持水平,重力加速度为
;求
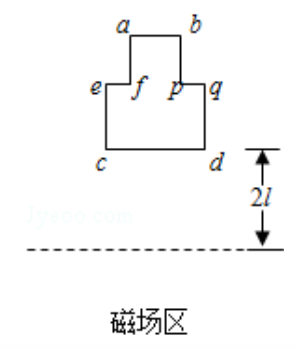
(1)线框
边将离开磁场时做匀速运动的速度大小是
边刚进入磁场时的几倍
(2)磁场上下边界间的距离
如图甲所示,abcd是位于竖直平面内的正方形闭合金属线框,在金属线框的下方有一磁感应强度为B的匀强磁场区域,MN和M′N′是匀强磁场区域的水平边界,边界的宽度为S,并与线框的bc边平行,磁场方向与线框平面垂直.现让金属线框由距MN的某一高度从静止开始下落,图乙是金属线框由开始下落到完全穿过匀强磁场区域的v-t图象(其中OA、BC、DE相互平行)。已知金属线框的边长为L(L<S)、质量为m,电阻为R,当地的重力加速度为g,图象中坐标轴上所标出的字母v1、v2、t1、t2、t3、t4均为已知量.(下落过程中bc边始终水平)根据题中所给条件,以下说法正确的是: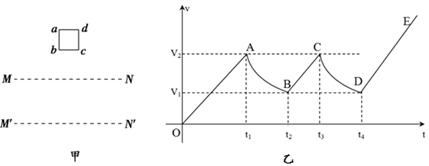
A.t2是线框全部进入磁场瞬间,t4是线框全部离开磁场瞬间
B.从bc边进入磁场起一直到ad边离开磁场为止,感应电流所做的功为mgS
C.V1的大小可能为
D.线框穿出磁场过程中流经线框横截面的电荷量比线框进入磁场过程中流经框横截面的电荷量多
一圆环形铝质金属圈(阻值不随温度变化)放在匀强磁场中,设第1s内磁感线垂直于金属圈平面(即垂直于纸面)向里,如图甲所示。若磁感应强度B随时间t变化的关系如图乙所示,那么第3s内金属圈中( )
| A.感应电流逐渐增大,沿逆时针方向 |
| B.感应电流恒定,沿顺时针方向 |
| C.圆环各微小段受力大小不变,方向沿半径指向圆心 |
| D.圆环各微小段受力逐渐增大,方向沿半径指向圆心 |
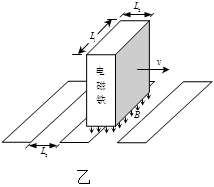
电磁阻尼制动是一种利用电磁感应原理工作的新型制动方式,它的基本原理如图甲所示。水平面上固定一块铝板,当一竖直方向的条形磁铁在铝板上方几毫米高度上水平经过时,铝板内感应出的电流会对磁铁的运动产生阻碍作用。电磁阻尼制动是磁悬浮列车在高速运行时进行制动的一种方式,某研究所制成如图乙所示的车和轨道模型来定量模拟磁悬浮列车的制动过程。车厢下端安装有电磁铁系统,能在长为L1=0.6m,宽L2=0.2m的矩形区域内产生竖直方向的匀强磁场,磁感应强度可随车速的减小而自动增大(由车内速度传感器控制),但最大不超过B1=2T,将铝板简化为长大于L1,宽也为L2的单匝矩形线圈,间隔铺设在轨道正中央,其间隔也为L2,每个线圈的电阻为R1=0.1Ω,导线粗细忽略不计。在某次实验中,模型车速度为v0=20m/s时,启动电磁铁系统开始制动,车立即以加速度a1=2m/s2做匀减速直线运动,当磁感应强度增加到B1时就保持不变,直到模型车停止运动。已知模型车的总质量为m1=36kg,空气阻力不计。不考虑磁感应强度的变化引起的电磁感应现象以及线圈激发的磁场对电磁铁产生磁场的影响。

(1)电磁铁的磁感应强度达到最大时,模型车的速度v1为多大?
(2)模型车的制动距离为多大?
(3)某同学受到上述装置的启发,设计了进一步提高制动效果的方案如下,将电磁铁换成多个并在一起的永磁铁组,两个相邻的磁铁磁极的极性相反,且将线圈改为连续铺放,相邻线圈接触紧密但彼此绝缘,如图丙所示,若永磁铁激发的磁感应强度恒定为B2,模型车质量m1及开始减速的初速度v0均不变,试通过必要的公式分析这种设计在提高制动能力上的合理性。
如图,竖直平面内放着两根间距L = 1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R= 2Ω的电阻,N板上有一小孔Q,在金属板M、N及CD上方有垂直纸面向里的磁感应强度B0= 1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T。有一质量M = 0.2kg、电阻r =1Ω的金属棒搭在MN之间并与MN良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点静止释放一个比荷 的正离子,经电场加速后,以v =200m/s的速度从Q点垂直于N板边界射入右侧区域。不计离子重力,忽略电流产生的磁场,取g=
的正离子,经电场加速后,以v =200m/s的速度从Q点垂直于N板边界射入右侧区域。不计离子重力,忽略电流产生的磁场,取g= 。求:
。求: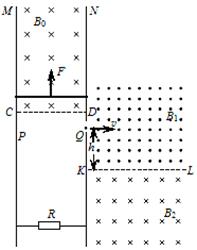
(1)金属棒达最大速度时,电阻R两端电压U;
(2)电动机的输出功率P;
(3)离子从Q点进入右侧磁场后恰好不会回到N板,Q点距分界线高h等于多少。
如图所示,正方形导线框ABCD、abcd的边长均为L,电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,且正方形导线框与定滑轮处于同一竖直平面内。在两导线框之间有一宽度为2L、磁感应强度大小为B、方向垂直纸面向里的匀强磁场。开始时导线框ABCD的下边与匀强磁场的上边界重合,导线框abcd的上边到匀强磁场的下边界的距离为L。现将系统由静止释放,当导线框ABCD刚好全部进入磁场时,系统开始做匀速运动。不计摩擦和空气阻力,则 ( )
A.两线框刚开始做匀速运动时轻绳上的张力FT=mg
B.系统匀速运动的速度大小:
C.两线框从开始运动至等高的过程中所产生的总焦耳热
D.导线框abcd通过磁场的时间
截流长直导线周围磁场的磁感应强度大小为 ,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为
,式中常量k>0,I为电流强度,r为距导线的距离。在水平长直导线MN正下方,矩形线圈abcd通以逆时针方向的恒定电流,被两根等长的轻质绝缘细线静止地悬挂,如图所示。开始时MN内不同电流,此时两细线内的张力均为 。当MN通以强度为
。当MN通以强度为 的电流时,两细线内的张力均减小为
的电流时,两细线内的张力均减小为 ,当MN内的电流强度变为
,当MN内的电流强度变为 时,两细线的张力均大于
时,两细线的张力均大于

(1)分别指出强度为 的电流和方向;
的电流和方向;
(2)MN分别通以强度为 电流时,线框受到的安培力
电流时,线框受到的安培力 大小之比。
大小之比。
如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B,圆台母线与竖直方向的夹角为θ。一个质量为m、半径为r的匀质金属圆环位于圆台底部。圆环中维持恒定的电流I,圆环由静止向上运动,经过时间t后撤去该恒定电流并保持圆环闭合,圆环上升的最大高度为H。已知重力加速度为g,磁场的范围足够大。在圆环向上运动的过程中,下列说法正确的是
| A.在最初t时间内安培力对圆环做的功为mgH |
B.圆环运动的最大速度为 |
| C.圆环先做匀加速运动后做匀减速运动 |
| D.圆环先有扩张后有收缩的趋势 |
如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻均不计。导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T。将一根质量为m=0.05kg有一定阻值的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好。现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行。(sin37°=0.6,cos37°=0.8)。求:
(1)金属棒与导轨间的动摩擦因数μ
(2)cd离NQ的距离s
(3)金属棒滑行至cd处的过程中,电阻R上产生的热量
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,为使金属棒中不产生感应电流,则磁感应强度B应怎样随时间t变化(写出B与t的关系式)。
如图所示,在倾角为37°的光滑斜面上有一根长为0.4 m,质量为6×10-2 kg的通电直导线,电流强度I=1 A,方向垂直于纸面向外,导线用平行于斜面的轻绳拴住不动,整个装置放在磁感应强度每秒增加0.4 T,方向竖直向上的磁场中.设t=0时,B=0,则需要多长时间斜面对导线的支持力为零?(g取10 m/s2)
如图所示,在倾角为θ=30°的斜面上,固定一宽L=0.25m的平行金属导轨,在导轨上端接入电源和变阻器.电源电动势E=12V,内阻r=1.0Ω一质量m=20g的金属棒ab与两导轨垂直并接触良好.整个装置处于磁感强度B=0.80T、垂直于斜面向上的匀强磁场中(导轨与金属棒的电阻不计).金属导轨是光滑的,取g=10m/s2,要保持金属棒在导轨上静止,求:
(1)金属棒所受到的安培力;
(2)通过金属棒的电流;
(3)滑动变阻器R接入电路中的阻值.