如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻均不计。导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻。有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T。将一根质量为m=0.05kg有一定阻值的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好。现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行。(sin37°=0.6,cos37°=0.8)。求:
(1)金属棒与导轨间的动摩擦因数μ
(2)cd离NQ的距离s
(3)金属棒滑行至cd处的过程中,电阻R上产生的热量
(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,为使金属棒中不产生感应电流,则磁感应强度B应怎样随时间t变化(写出B与t的关系式)。
如图甲所示,电阻不计的光滑平行金属导轨固定在水平面上,导轨间距L="0.5" m,左端连接R="0.5" Ω的电阻,右端连接电阻不计的金属卡环。导轨间MN右侧存在方向垂直导轨平面向下的磁场.磁感应强度的B-t图象如图乙所示。电阻不计质量为m="1" kg的金属棒与质量也为m的物块通过光滑滑轮由绳相连,绳始终处于绷紧状态。PQ、MN到右端卡环距离分别为17.5 m和15 m。t=0时刻由PQ位置静止释放金属棒,金属棒与导轨始终接触良好,滑至导轨右端被卡环卡住不动。(g取10 m/s2)求:
(1)金属棒进入磁场时受到的安培力
(2)在0~6 s时间内电路中产生的焦耳热
如图所示,宽度为L的金属框架竖直固定在绝缘地面上,框架的上端接有一特殊的电子元件,如果将其作用等效成一个电阻,则其阻值与其两端所加的电压成正比,即等效电阻R=kU,式中k为恒量。框架上有一质量为m的金属棒水平放置,金属棒与框架接触良好无摩擦,离地高为h,磁感应强度为B的匀强磁场与框架平面相垂直,将金属棒由静止释放,金属棒沿框架向下运动。不计金属棒及框架电阻,问: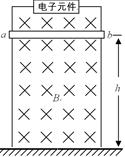
⑴金属棒运动过程中,流过金属棒的电流多大?方向如何?
⑵金属棒经多长时间落到地面?金属棒下落过程中整个电路消耗的电能为多少?
如图甲,单匝圆形线圈c与电路连接,电阻R2两端与平行光滑金属直导轨p1e1f1、p2e2f2连接.垂直于导轨平面向下、向上有矩形匀强磁场区域Ⅰ、Ⅱ,它们的边界为e1e2,区域Ⅰ中垂直导轨并紧靠e1e2平放一导体棒ab.两直导轨分别与同一竖直平面内的圆形光滑绝缘导轨o1、o2相切连接,o1、o2在切点f1、f2处开有小口可让ab进入,ab进入后小口立即闭合.已知:o1、o2的直径和直导轨间距均为d,c的直径为2d;电阻R1、R2的阻值均为R,其余电阻不计;直导轨足够长且其平面与水平面夹角为 ,区域Ⅰ的磁感强度为B0.重力加速度为g.在c中边长为d的正方形区域内存在垂直线圈平面向外的匀强磁场,磁感强度B随时间t变化如图乙所示,ab在t=0~
,区域Ⅰ的磁感强度为B0.重力加速度为g.在c中边长为d的正方形区域内存在垂直线圈平面向外的匀强磁场,磁感强度B随时间t变化如图乙所示,ab在t=0~ 内保持静止.
内保持静止.
(1)求ab静止时通过它的电流大小和方向;
(2)求ab的质量m;
(3)设ab进入圆轨道后能达到离f1f2的最大高度为h,要使ab不脱离圆形轨道运动,求区域Ⅱ的磁感强度B2的取值范围并讨论h与B2的关系式.
如图,竖直平面内放着两根间距L = 1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R= 2Ω的电阻,N板上有一小孔Q,在金属板M、N及CD上方有垂直纸面向里的磁感应强度B0= 1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T。有一质量M = 0.2kg、电阻r =1Ω的金属棒搭在MN之间并与MN良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点静止释放一个比荷 的正离子,经电场加速后,以v =200m/s的速度从Q点垂直于N板边界射入右侧区域。不计离子重力,忽略电流产生的磁场,取g=
的正离子,经电场加速后,以v =200m/s的速度从Q点垂直于N板边界射入右侧区域。不计离子重力,忽略电流产生的磁场,取g= 。求:
。求:
(1)金属棒达最大速度时,电阻R两端电压U;
(2)电动机的输出功率P;
(3)离子从Q点进入右侧磁场后恰好不会回到N板,Q点距分界线高h等于多少。
如图所示,两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2、…、n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B、…、nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻。
(1)对导体棒ab施加水平向右的力,使其从图示位置开始运动并穿过n个磁场区,求导体棒穿越磁场区1的过程中通过电阻R的电荷量q;
(2)对导体棒ab施加水平向右的恒力F0,让它从磁场区1左侧边界处开始运动,当向右运动距 时做匀速运动,求棒通过磁场区1所用的时间t;
时做匀速运动,求棒通过磁场区1所用的时间t;
(3)对导体棒ab施加水平向右的拉力,让它从距离磁场区1左侧x=x0的位置由静止开始做匀加速运动,当棒ab进入磁场区1时开始做匀速运动,此后在不同的磁场区施加不同的拉力,使棒ab保持做匀速运动穿过整个磁场区,求棒ab通过第i磁场区时的水平拉力Fi和棒ab在穿过整个磁场区过程中回路产生的电热Q。
均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m,将其置于磁感应强度为B的水平匀强磁场上方h处,如图所示,线框由静止自由下落,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界平行,当cd边刚进入磁场时,求:
(1)cd两点间的电势差大小,C.d两点哪点的电势较高
(2)若此时线框计数点恰好为零,求线框下落的高度h所应满足的条件
如图所示,凸字形硬质金属线框质量为
,相邻各边互相垂直,且处于同一竖直平面内,
边长为
,
边长为
,
与
平行,间距为
。匀强磁场区域的上下边界均水平,磁场方向垂直于线框所在平面。开始时,
边到磁场上边界的距离为
,线框由静止释放,从
边进入磁场直到
、
边进入磁场前,线框做匀速运动,在
、
边离开磁场后,
边离开磁场之前,线框又做匀速运动。线框完全穿过磁场过程中产生的热量为
。线框在下落过程中始终处于原竖直平面内,且
.
边保持水平,重力加速度为
;求
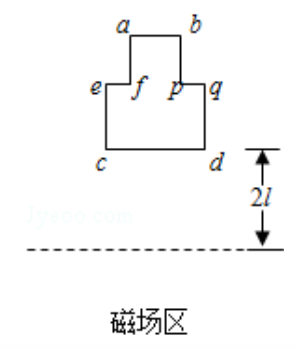
(1)线框
边将离开磁场时做匀速运动的速度大小是
边刚进入磁场时的几倍
(2)磁场上下边界间的距离
如图所示,两根电阻不计的光滑金属导轨MAC.NBD水平放置,MA.NB间距L=0.4m,AC.BD的延长线相交于E点且AE=BE,E点到AB的距离d=6m,M、N两端与阻值R=2Ω的电阻相连,虚线右侧存在方向与导轨平面垂直向下的匀强磁场,磁感应强度B=1T。一根长度也为L=0.4m、质量m=0.6kg、电阻不计的金属棒,在外力作用下从AB处以初速度 沿导轨水平向右运动,棒与导轨接触良好,运动过程中电阻R上消耗的电功率不变,求:
沿导轨水平向右运动,棒与导轨接触良好,运动过程中电阻R上消耗的电功率不变,求:
(1)电路中的电流I;
(2)金属棒向右运动d/2过程中克服安培力做的功W;
水平面上有电阻不计的U形导轨MNPQ,宽度为L,N和P之间接入电动势为E的电源(不计内阻)。现垂直导轨放置质量为m、电阻为R的金属棒ab,金属棒与导轨间的动摩擦因数为μ,并加范围较大的、磁感应强度大小为B匀强磁场,磁场方向与水平面夹角为θ且指向右上方,如图所示。求:
(1)当ab棒静止时,ab棒受到的支持力和摩擦力各为多少?
(2)若B的大小和方向均能改变,则要使ab棒所受支持力为零,B的大小至少为多少?此时B的方向如何?
(3)若B的大小和方向均能改变,则要使ab棒恰好处于静止状态,B的大小至少为多少?此时B的方向如何?
如图所示,质量为2m的 U形线框ABCD下边长度为L,电阻为R,其它部分电阻不计,其内侧有质量为m,电阻为R的导体棒PQ,PQ与线框相接触良好,可在线框内上下滑动。整个装置竖直放置,其下方有垂直纸面的匀强磁场,磁感应强度为B。将整个装置从静止释放,在下落过程线框底边始终水平。当线框底边进入磁场时恰好做匀速运动,此时导体棒PQ与线框间的滑动摩擦力为 。经过一段时间,导体棒PQ恰好到达磁场上边界,但未进入磁场,PQ运动的距离是线框在磁场中运动距离的两倍。不计空气阻力,重力加速度为g。求:
。经过一段时间,导体棒PQ恰好到达磁场上边界,但未进入磁场,PQ运动的距离是线框在磁场中运动距离的两倍。不计空气阻力,重力加速度为g。求:
(1)线框刚进入磁场时,BC两端的电势差;
(2)导体棒PQ到达磁场上边界时速度大小;
(3)导体棒PQ到达磁场上边界前的过程线框中产生的焦耳热。
如图所示,在竖直平面内有宽度为L足够长的金属导轨,导轨间有垂直纸面向里的匀强磁场,磁感应强度大小为B0,导轨上有一导体棒在外力作用下以速度v0向左匀速运动;P、Q为竖直平面内两平行金属板,分别用导线和M、N相连,P、Q板长为d,间距也为d, P、Q板间虚线右侧为垂直纸面向里的匀强磁场,磁感应强度大小为B。现有一电量为q的带正电小球,从P、Q左边界的中点水平射入,进入磁场后做匀速圆周运动,重力加速度取g。求:
(1)带电小球的质量m;
(2)能够打在P板上的带电小球在磁场中运动的最短时间;
(3)能够打在P板上的带电小球速度v的取值范围。
如图所示,顶角θ=45°的金属导轨MON固定在水平面内,导轨处在方向竖直向下、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均为r.导体棒与导轨接触点为a和b,导体棒在滑动过程中始终保持与导轨良好接触.t=0时导体棒位于顶角O处,则流过导体棒的电流强度I、导体棒内产生的焦耳热Q、导体棒做匀速直线运动时水平外力F、导体棒的电功率P各量大小随时间变化的关系正确的是

如图所示,在匀强磁场中有一足够长的光滑平行金属导轨,与水平面间的夹角θ=30°,间距L=0.5m,上端接有阻值R=0.3Ω的电阻.匀强磁场的磁感应强度大小B=0.4T,磁场方向垂直导轨平面向上.一质量m=0.2kg,电阻r=0.1Ω的导体棒MN,在平行于导轨的外力F作用下,由静止开始向上做匀加速运动,运动过程中导体棒始终与导轨垂直,且接触良好.当棒的位移d=9m时,电阻R上消耗的功率为P=2.7W.其它电阻不计, g取10 m/s2.求: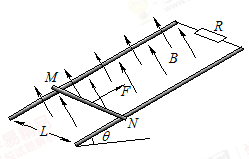
(1)此时通过电阻R上的电流;
(2)这一过程通过电阻R上的电荷量q;
(3)此时作用于导体棒上的外力F的大小.
如图所示,质量为M=2kg的足够长的U型金属框架abcd,放在光滑绝缘水平面上,导轨ab边宽度L=1m。电阻不计的导体棒PQ,质量m=1kg,平行于ab边放置在导轨上,并始终与导轨接触良好,棒与导轨间动摩擦因数μ=0.5,棒左右两侧各有两个固定于水平面上的光滑立柱。开始时PQ左侧导轨的总电阻R=1Ω,右侧导轨单位长度的电阻为r0=0.5Ω/m。以ef为界,分为左右两个区域,最初aefb构成一正方形,g取10m/s2。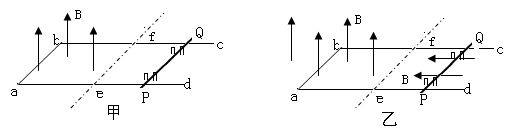
(1)如果从t=0时,在ef左侧施加B=kt(k=2T/s),竖直向上均匀增大的匀强磁场,如图甲所示,多久后金属框架会发生移动(设最大静摩擦力等于滑动摩擦力).
(2)如果ef左右两侧同时存在B=1T的匀强磁场,方向分别为竖直向上和水平向左,如图乙所示。从t=0时,对框架施加一垂直ab边的水平向左拉力,使框架以a=0.5m/s2向左匀加速运动,求t=2s时拉力F多大
(3)在第(2)问过程中,整个回路产生的焦耳热为Q=0.6J,求拉力在这一过程中做的功。