高中物理判断洛伦兹力的方向试题

下列各图中，运动电荷的速度方向、磁场方向和电荷的受力方向之间的关系正确的是（  ）

将一束等离子体（即高温下电离的气体，含有大量带正电和带负电的微粒，而从整体上来说呈电中性）喷入磁场，由于等离子体在磁场力的作用下运动方向发生偏转，磁场中的两块金属板A和B上就会聚集电荷，从而在两板间产生电压.在图示磁极配置的情况下，下列表述正确的是

A．金属板A的电势较高
B．通过电阻R的电流方向是b→R→a
C．等离子体在A、B间运动时，磁场力对等离子体做正功                  
D．等离子体在A、B间运动时，磁场力对等离子体不做功

从太阳或其他星体上放射出的宇宙射线中含有大量的高能带电粒子，这些高能粒子流到达地球会对地球上的生命带来危害，但是由于地球周围存在磁场，地磁场能改变宇宙射线中带电粒子的运动方向，对地球上的生命起到保护作用，如图，那么

A．地磁场对宇宙射线的阻挡作用各处相同

B．地磁场对垂直射向地球表面的宇宙射线的阻挡作用在南、北两极最强，赤道附近最弱

C．地磁场对垂直射向地球表面的宇宙射线的阻挡作用在南、北两极最弱，赤道附近最强

D．地磁场会使沿地球赤道平面内射来的宇宙射线中的带电粒子向两极偏转

下列说法正确的是（    ）

A．运动电荷在磁感应强度不为零的地方，一定受到洛伦兹力的作用

B．运动电荷在某处不受洛伦兹力的作用，则该处的磁感应强度一定为零

C．洛伦兹力既不能改变带电粒子的动能，也不能改变带电粒子的速度

D．洛伦兹力对带电粒子不做功

显像管的工作原理图如图所示，图中阴影区域没有磁场时，从电子枪发出的电子打在荧光屏正中的O点．为使电子在竖直方向偏离中心，打在荧光屏上的A点，阴影区域所加磁场的方向是

A．竖直向上

B．竖直向下

C．垂直于纸面向内

D．垂直于纸面向外

初速度为v₀的电子，沿平行于通电长直导线的方向射出，直导线中电流方向与电子的初始运动方向如图所示，则(       )

A．电子将向右偏转，速率不变	B．电子将向右偏转，速率改变
C．电子将向左偏转，速率不变	D．电子将向左偏转，速率改变

如图所示，正方形abcd区域内有垂直于纸面向里的匀强磁场，O点是cd边的中点。   一个带正电的粒子(重力忽略不计）从O点沿纸面以垂直于cd边的速度射入正方形区域内，经过时间t₀刚好从c点射出磁场。现设法使该带电粒子从O点沿纸面以与Od成30°的方向(如图中虚线所示），以各种不同的速率射入正方形内，那么下列说法正确的是

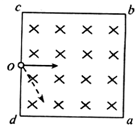
A．该带电粒子不可能刚好从正方形的某个顶点射出磁场

B．若该带电粒子从ab边射出磁场，它在磁场中经历的时间可能是t0

C．若该带电粒子从bc边射出磁场，它在磁场中经历的时间可能是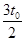

D．若该带电粒子从cd边射出磁场，它在磁场中经历的时间一定是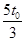

以下说法中，正确的是

A．电荷处于磁场中一定受到洛伦兹力

B．运动电荷在磁场中一定受到洛伦兹力

C．洛伦兹力对运动电荷一定不做功

D．洛伦兹力可以改变运动电荷的速度方向

如图所示,从MN上方存在匀强磁场，带同种电荷的粒子a、b以相同的动能同时从O点射入匀强磁场中，两粒子的入射方向与磁场边界MN的夹角分别为30^o和60^o，且同时到达P点，已知OP=d，则（   ）

A．a、b两粒子运动半径之比为1：

B．a、b两粒子的初速率之比为5：2

C．a、b两粒子的质量之比为4：75

D．a、b两粒子的电荷量之比为2：15

如图所示，S处有一电子源，可向纸面内任意方向发射电子，平板MN垂直于纸面，在纸面内的长度L=9.1cm，中点O与S间的距离d=4.55cm，MN与SO直线的夹角为θ，板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场，磁感应强度B=2.0×10^﹣4T．电子质量m=9.1×10^﹣31kg，电量e=1.6×10^﹣19C，不计电子重力．电子源发射速度v=1.6×10⁶m/s的一个电子，该电子打在板上可能位置的区域的长度为l，则（ ）

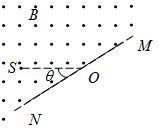
A．θ=90°时，l=9.1cm	B．θ=60°时，l=9.1cm
C．θ=45°时，l=4.55cm	D．θ=30°时，l=4.55cm

关于磁场中的通电导线和运动电荷的有关说法中正确的是(       )      

A．磁场对通电导线的作用力方向一定与磁场方向垂直

B．通电导线在磁场中一定会受到安培力的作用

C．带电粒子在磁场中也可能做匀速直线运动

D．在磁场中运动的带电粒子，其动能一定不变，而速度一定变化

关于安培力和洛伦兹力，下面说法正确的是（   ）

A．洛伦兹力和安培力是性质完全不同的两种力

B．安培力和洛伦兹力，其本质都是磁场对运动电荷的作用力

C．安培力和洛伦兹力，二者是等价的

D．安培力对通电导体能做功，但洛伦兹力对运动电荷不能做功

用磁场可以约束带电离子的轨迹，如图所示，宽d=2cm的有界匀强磁场的横向范围足够大，磁感应强度方向垂直纸面向里，B=1T．现有一束带正电的粒子从O点以v=2×10⁶m/s的速度沿纸面垂直边界进入磁场．粒子的电荷量q=1.6×10^﹣19C，质量m=3.2×10^﹣27kg．求：

（1）粒子在磁场中运动的轨道半径r和运动时间t是多大？
（2）粒子保持原有速度，又不从磁场上边界射出，则磁感应强度最小为多大？

如图所示的正方形的盒子开有a、b、c三个微孔，盒内有垂直纸面向里的匀强磁场，一束速率不同的电子从a孔沿垂直于磁感线方向射入盒中，发现从c孔和b孔有电子射出．则

（1）从b孔和c孔射出的电子的速率之比V_b：V_c为      ；
（2）从b孔和c孔射出的电子在盒内运动时间之比 为      ．

一个带电粒子以某一初速度射入匀强磁场中，不考虑其它力的作用，粒子在磁场中不可能做（ ）

A．匀速直线运动	B．匀变速直线运动
C．匀变速曲线运动	D．匀速圆周运动