高中物理判断洛伦兹力的方向试题

如图所示，在区域足够大的空间中充满磁感应强度大小为B的匀强磁场，其方向垂直于纸面向里，在纸面内固定放置一绝缘材料制成的边长为L的等边三角形框架DEF，DE中点S处有一粒子发射源，发射粒子的方向皆在图中截面内且垂直于DE边向下如图（a）所示，发射粒子的电量为+q质量为m，但速度v有各种不同的数值。若这些粒子与三角形框架碰撞时均无能量损失，并要求每一次碰撞时速度方向垂直于被碰的边，试求：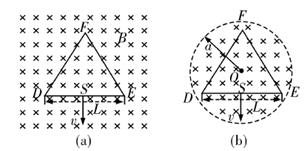

（1）带电粒子的速度v为多大时能够不与框架碰撞打到E点？
（2）为使S点发出的粒子最终又回到S点，且运动时间最短，v应为多大？最短时间为多少？
（3）若磁场是半径为a的圆柱形区域如图（b）所示（图中圆为其横截面），圆柱的轴线通过等边三角形的中心O，且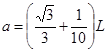，要使S点发出的粒子最终又回到S点带电粒子速度v的大小应取哪些数值？

如图所示，绝缘轨道由弧形轨道和半径为R=0.16m的圆形轨道、水平轨道连接而成，处于竖直面内的匀强电场中，PQ左右两侧电场方向相反，其中左侧方向竖直向下，场强大小均为10³V/m，不计一切摩擦。质量为m=0.1kg的带正电小球可看作质点）从弧形轨道某处由静止释放，恰好能通过圆形轨道最高点，小球带电荷量q="1." 0×10^-3C，g取10m/s²。求：

（1）小球释放点的高度h
（2）若PQ右侧某一区域存在垂直纸面向里的匀强磁场（图中未画出），磁感应强度B=4×10²T，小球通过圆形轨道后沿水平轨道运动到P点进入磁场，从竖直边界MN上的A点离开时速度方向与电场方向成30^o，已知PQ、MN边界相距L=0.7m，求：
①小球从P到A经历的时间
②若满足条件的磁场区域为一矩形，求最小的矩形面积。

如图所示，在圆形区域内存在垂直纸面向外的匀强磁场，ab是圆的直径。一带电粒子从a点射入磁场，速度大小为v、方向与ab成30°角时，恰好从b点飞出磁场，且粒子在磁场中运动的时间为t；若同一带电粒子从a点沿ab方向射入磁场，也经时间t飞出磁场，则其速度大小为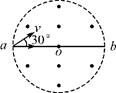

A．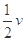

B．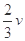

C．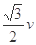

D．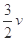

（多选题）某空间存在方向垂直于纸面向里的矩形匀强磁场abcd，ad =L，ab =2L．一细束由两种粒子组成的粒子流沿垂直于磁场的方向从ad边的中点O垂直于ad边入射．粒子均带正电荷，它们的电荷量、质量均不同，但其比荷相同，且都包含不同速率的粒子（不计粒子重力）．下列说法正确的是（ ）

A．入射速度不同的粒子在磁场中的运动时间一定不同

B．入射速度不同的粒子在磁场中的运动时间可能相同

C．从a点射出的粒子与从b点射出的粒子的运动半径之比为1:17

D．从a点射出的粒子与从b点射出的粒子的运动半径之比为2:17

如图所示，在xoy坐标系中，以（r，0）为圆心、r为半径的圆形区域内存在匀强磁场，磁场的磁感应强度大小为B，方向垂直于纸面向里。在y>r的足够大的区域内，存在沿y轴负方向的匀强电场，场强大小为E。从O点以相同速率向不同方向发射质子，质子的运动轨迹均在纸面内，且质子在磁场中运动的轨迹半径也为r。已知质子的电荷量为q，质量为m，不计质子所受重力及质子间相互作用力的影响。

（1）求质子射入磁场时速度的大小；
（2）若质子沿x轴正方向射入磁场，求质子从O点进入磁场到第二次离开磁场经历的时间；
（3）若质子沿与x轴正方向成夹角θ的方向从O点射入第一象限的磁场中，求质子在磁场中运动的总时间。

如图所示的圆形区域内有匀强磁场，其边界跟y轴在坐标原点O处相切；磁感应强度为B，方向垂直于纸面向里，在O处有一放射源可沿纸面向各个方向射出速率均为v的带电粒子；已知带电粒子质量为m，电荷量q，圆形磁场区域的半径 ,则粒子在磁场中运动的最长时间是多少？

如图所示，在平面直角坐标系xoy内，第一象限存在沿y轴负方向的匀强电场，一质量为m，电荷量为q的带正电的粒子，从y轴正半轴上y=d处的M点，以速度v₀垂直于y轴射入电场，经x轴上处的N点进入第四象限，在第四象限适当区域内存在方向垂直于纸面向外的匀强磁场，磁感应强度为B，已知此磁场仅分布在一个圆形区域内（图中未画出），粒子进入磁场后，最后以垂直于y轴的方向射出磁场，不计粒子重力。求：

（1）电场强度的大小E；
（2）粒子在N点时的速度大小和方向；
（3）粒子在磁场中运动时间；
（4）圆形区域的最小面积。

如图所示，足够长粗糙绝缘细杆水平放置，其上套有一带正电荷，质量为m的小球，装置处在垂直于纸面向里的匀强磁场中。现使小球以大小为v₀，方向水平向右的初速度运动，则小球在整个运动过程中，关于小球机械能的损失量结论正确的是

A．不可能为0

B．可能为

C．可能为

D．可能为

汤姆孙提出的测定带电粒子的比荷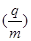的实验原理如图所示。带电粒子经过电压为U的加速电场加速后，垂直于磁场方向进入宽为L的有界匀强磁场，带电粒子穿过磁场时发生的偏转位移是d，若磁场的磁感应强度为B。则带电粒子的比荷为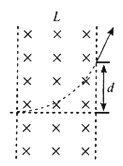

A.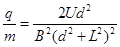
B.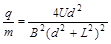
C.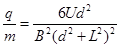
D.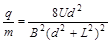

如图所示，在xOy坐标系y轴右侧有垂直于纸面向里的匀强磁场，磁感应强度为B，在第四象限还有沿x轴负方向的匀强电场，y轴上有一点P，坐标已知为（0，L），一电荷量为q、质量为m的粒子从P点以某一大小未知的速度沿与y轴正方向夹角为30°的方向垂直射入磁场，已知粒子能够进入第四象限，并且在其中恰好做匀速直线运动。不计重力，求：

（1）粒子在第一象限中运动的时间t；
（2）电场强度E。

如图是质谱仪工作原理的示意图。带电粒子a、b从容器中的A点飘出（在A点初速度为零），经电压U加速后，从x轴坐标原点处垂直进入磁感应强度为B的匀强磁场，最后打在放在x轴上感光板S上坐标分别为x₁、x₂的两点。图中半圆形的虚线分别表示带电粒子a、b所通过的路径，则以下说法正确的是 （   ）

A．b进入磁场时的速度一定大于a进入磁场时的速度

B．a的比荷一定小于b的比荷

C．若a、b电荷量相等，则a、b的质量之比为x1^2∶x2^2

D．若a、b质量相等，则a、b在磁场中运动时间之比为x1∶x2

在一个边界为等边三角形的区域内，存在一个方向垂直于纸面向里的匀强磁场，在磁场边界上的P点处有一个粒子源，发出比荷相同的三个粒子a、b、c（不计重力）沿同一方向进入磁场，三个粒子通过磁场的轨迹如图所示，用t_a、t_b、t_c分别表示a、b、c通过磁场的时间；用r_a、r_b、r_c分别表示a、b、c在磁场中的运动半径，则下列判断正确的是（ ）

A．ta=tb＞tc

B．tc＞tb＞ta

C．rc＞rb＞ra

D．rb＞ra＞rc

带电粒子在磁场中运动，洛伦兹力对带电粒子        （填“做正功”、“做负功”或“不做功”），原因是      ．

如图所示，xOy坐标平面中的直角三角形ACD区域，AC与CD长度均为l，且A、C、D均位于坐标轴上，区域内有垂直于坐标平面向里的匀强磁场，磁感应强度大小为B．坐标原点O处有一粒子源，粒子源能够从O点沿x轴正方向发射出大量带正电的同种粒子，不计粒子重力及粒子间相互作用，粒子的比荷为，发现恰好所有粒子都不能从AC边射出，求这些粒子中速度的最大值．

每时每刻都有大量宇宙射线向地球射来，地磁场可以改变射线中大多数带电粒子的运动方向，使它们不能到达地面，这对地球上的生命有十分重要的意义，下列有关说法正确的是（ ）

A．在北极竖直向下射向地球的带电粒子不会发生偏转

B．在赤道竖直向下射向地球的带正电的粒子会向南偏转

C．在赤道竖直向下射向地球的带负电的粒子会向西偏转

D．在南极竖直向下射向地球的带电粒子会向北发生偏转