如图所示,一个静止的质量为m、带电荷量为q的粒子(不计重力),经电压U加速后垂直进人磁感应强度为B的匀强磁场,粒子在磁场中转半个国后打在P点,设OP=x,能够正确反应x与U之间的函数关系的是

如图所示,在平面直角坐标系xOy中,第Ⅰ象限内有沿y轴负向的匀强电场,电场强度的大小为E,第Ⅳ象限内有垂直纸面向外的匀强电场。在y轴上的P点沿x轴正向发射质量为m、电荷量为q的带正电粒子,粒子从x轴上Q点射入磁场。已知Q点坐标为(L,0),不计粒子的重力及相互作用。
(1)若粒子在Q点的速度方向与x轴成30°角,求P点的坐标及粒子在Q点的速度大小;
(2)若从y轴的正半轴上各点处均向x轴正向发射与(1)中相同的粒子,结果这些粒子均能从x轴上的Q点进入磁场,并且到Q点速度最小的粒子A,经磁场偏转后,恰好垂直y轴射出磁场,求匀强磁场的磁感应强度大小及粒子A在磁场中运动时间。
如图所示,相距为R的两块平行金属板M、N正对着放置, S1、S2分别为M、N板上的小孔,S1、S2、O三点共线,它们的连线垂直M、N,且S2O=R。以O为圆心、R为半径的圆形区域内存在磁感应强度为B、方向垂直纸面向外的匀强磁场。D为收集板,板上各点到O点的距离以及板两端点的距离都为2R,板两端点的连线垂直M、N板。质量为m、带电荷量为+q的粒子经S1进入M、N间的电场后,通过S2进入磁场。粒子在S1处的速度和粒子所受的重力均不计。
(1)当M、N间的电压为U时,求粒子进入磁场时速度的大小v;
(2)若粒子恰好打在收集板D的中点上,求M、N间的电压值U0;
(3)当M、N间的电压不同时,粒子从S1到打在D上经历的时间t会不同,求t的最小值。
如图所示,在坐标系xOy中,第一象限除外的其它象限都充满匀强磁场,磁感应强度都为B=0.12 T、方向垂直纸面向内。P是y轴上的一点,它到坐标原点O的距离l=0.40 m。一比荷 =5.0×107 C/kg的带正电粒子从P点开始进入匀强磁场中运动,初速度v0=3.0×106 m/s、方向与y轴正方向成夹角θ=53°并与磁场方向垂直。不计粒子的重力作用。已知sin 53°=0.8,cos 53°=0.6,求:
=5.0×107 C/kg的带正电粒子从P点开始进入匀强磁场中运动,初速度v0=3.0×106 m/s、方向与y轴正方向成夹角θ=53°并与磁场方向垂直。不计粒子的重力作用。已知sin 53°=0.8,cos 53°=0.6,求:
(1)粒子在磁场中运动的轨道半径R;
(2)在第一象限中与x轴平行的虚线上方的区域内充满沿x轴负方向的匀强电场(如图),粒子在磁场中运动一段时间后进入第一象限,最后恰好从P点沿初速度的方向再次射入磁场。求匀强电场的电场强度E和电场边界(虚线)与x轴之间的距离d。
如图所示,某空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,已知一离子在电场力和磁场力作用下,从静止开始沿曲线acb运动,到达b点时速度为零,c点为运动的最低点,则( )

| A.离子必带负电 |
| B.a、b两点位于同一高度 |
| C.离子在c点速度最大 |
| D.离子到达b点后将沿原曲线返回a点 |
如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为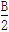 的匀强磁场。一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在上方磁场中运动半径为R,则( )
的匀强磁场。一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在上方磁场中运动半径为R,则( )

| A.粒子经偏转一定能回到原点O |
| B.粒子在x轴上方和下方两磁场中运动的半径之比为2∶1 |
| C.粒子完成一次周期性运动的时间为2πm/3qB |
| D.粒子第二次射入x轴上方磁场时,沿x轴前进3R |
如图所示,在边长为2a的正三角形区域内存在方向垂直于纸面向里的匀强磁场,一个质量为m、电荷量为-q的带电粒子(重力不计)从AB边的中点O以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与AB边的夹角为60°,若要使粒子能从AC边穿出磁场,则匀强磁场的大小B需满足( )

A.B< |
B.B< |
C.B> |
D.B< |
如图所示为质谱仪上的原理图,M为粒子加速器,电压为U1=5000V;N为速度选择器,磁场与电场正交,磁感应强度为B1=0.2T,板间距离为d=0.06m;P为一个边长为l的正方形abcd的磁场区,磁感应强度为B2=0.1T,方向垂直纸面向外,其中dc的中点S开有小孔,外侧紧贴dc放置一块荧光屏.今有一比荷为 =108C/kg的正离子从静止开始经加速后,恰好通过速度选择器,从a孔以平行于ab方向进入abcd磁场区,正离子刚好经过小孔S 打在荧光屏上.求:
=108C/kg的正离子从静止开始经加速后,恰好通过速度选择器,从a孔以平行于ab方向进入abcd磁场区,正离子刚好经过小孔S 打在荧光屏上.求:
(1)粒子离开加速器时的速度v;
(2)速度选择器的电压U2;
(3)正方形abcd边长l.
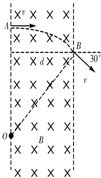
如图所示,有一对平行金属板,两板相距为0.05m.电压为10V;两板之间有匀强磁场,磁感应强度大小为B0=0.1T,方向与金属板面平行并垂直于纸面向里.图中右边有一半径R为0.1m、圆心为O的圆形区域内也存在匀强磁场,磁感应强度大小为 ,方向垂直于纸面向里.一正离子沿平行于金属板面,从A点垂直于磁场的方向射入平行金属板之间,沿直线射出平行金属板之间的区域,并沿直径CD方向射入圆形磁场区域,最后从圆形区域边界上的F点射出.已知速度的偏向角
,方向垂直于纸面向里.一正离子沿平行于金属板面,从A点垂直于磁场的方向射入平行金属板之间,沿直线射出平行金属板之间的区域,并沿直径CD方向射入圆形磁场区域,最后从圆形区域边界上的F点射出.已知速度的偏向角 ,不计离子重力.求:
,不计离子重力.求:
(1)离子速度v的大小;
(2)离子的比荷 ;
;
(3)离子在圆形磁场区域中运动时间t.
如图所示,一束电子(电量为e)以速度υ垂直射入磁感应强度为B,宽度为d的匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是 ,穿透磁场的时间是 .
如图所示,在边长为L的正方形区域内有垂直于纸面向里的匀强磁场,有一带正电的电荷,从D点以v0的速度沿DB方向射入磁场,恰好从A点射出,已知电荷的质量为m,带电量为q,不计电荷的重力,则下列说法正确的是( )

A.匀强磁场的磁感应强度为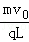 |
B.电荷在磁场中运动的时间为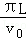 |
| C.若电荷从CD边界射出,随着入射速度的减小,电荷在磁场中运动的时间会减小 |
| D.若电荷的入射速度变为2v0,则粒子会从AB中点射出 |
如图所示,有一垂直于纸面向外的磁感应强度为B的有界匀强磁场(边界上有磁场),其边界为一边长为L的三角形,A、C、D为三角形的顶点.今有一质量为m、电荷量为+q的粒子(不计重力),以速度v= 从AD边上某点P既垂直于AD边、又垂直于磁场的方向射人磁场,然后从CD边上某点Q(图中未画出)射出.若从P点射入的该粒子能从Q点射出,则( )
从AD边上某点P既垂直于AD边、又垂直于磁场的方向射人磁场,然后从CD边上某点Q(图中未画出)射出.若从P点射入的该粒子能从Q点射出,则( )

A.|PD|≤ L B.|PD|≤
L B.|PD|≤ L C.|QD|≤
L C.|QD|≤ L D.|QD|≤
L D.|QD|≤ L
L
质量为m,电荷量为q的粒子,以初速度v垂直进入磁感应强度为B,宽度为L的匀强磁场区域,并从另一端出射,如图所示,不计粒子重力。求
(1)带电粒子运动的轨道半径R;
(2)带电粒子离开磁场时的偏转角的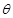 ;
;
(3)带电粒子在磁场中的运动时间t。
等离子气流由左方持续以 射入
射入 和
和 两板间的匀强磁场中,ab直导线与
两板间的匀强磁场中,ab直导线与 和
和 相连接,线圈A与直导线cd连接,线圈A内有随图乙所示的变化磁场,且磁场B的正方向规定为向左,如图甲所示,则下列叙述正确的是
相连接,线圈A与直导线cd连接,线圈A内有随图乙所示的变化磁场,且磁场B的正方向规定为向左,如图甲所示,则下列叙述正确的是
A.0-1s内aB.cd导线互相排斥
B.1-2s内aB.cd导线互相吸引
C.2-3s内aB.cd导线互相吸引
D.3-4s内aB.cd导线互相排斥