如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
(1)若P、Q间外加一与磁场方向垂直的匀强电场,能使速度为v0射出的微粒沿PQ直线运动到Q点,则场强为多大?
(2)撤去电场,为使微粒从P点射出后,途经折线的顶点A而到达Q点,求初速度v应满足什么条件?
(3)求第(2)中微粒从P点到达Q点所用时间的最小值.
关于磁感应强度,下列说法正确的是
A.若长度为L、电流为I的一小段通电直导线放入匀强磁场受到磁场力F,则该匀强磁场的磁感应强度大小为 |
| B.磁感应强度的方向与放入该点的电流元所受磁场力的方向相同 |
| C.磁感应强度的方向与放入该点小磁针N极所受磁场力的方向相同 |
D.由磁感应强度 可知,磁感应强度B与电流元在该点受到的磁场力F成正比,与电流元IL成反比 可知,磁感应强度B与电流元在该点受到的磁场力F成正比,与电流元IL成反比 |
两根长直导线a、b平行放置,如图所示为垂直于导线的截面图,图中O点为两根导线ab连线的中点,M、N为ab的中垂线上的两点且与a、b等距,两导线中通有等大、同向的恒定电流,已知直线电流在某点产生的磁场的磁感应强度B的大小跟该点到通电导线的距离r成反比,则下列说法中正确的是( )

| A.M点和N点的磁感应强度大小相等,方向相同 |
| B.M点和N点的磁感应强度大小相等,方向相反 |
| C.在线段MN上各点的磁感应强度都不可能为零 |
| D.若在N点放一小磁针,静止时其北极垂直MN向上 |
如图所示,固定于水平面上的金属架abcd处在竖直向下的匀强磁场中,金属棒MN沿框架以速度v向右做匀速运动。t=0时,磁感应强度为B=" 0" ,此时MN到达的位置恰好使MbcN构成一个边长为l的正方形。为使MN棒中不产生感应电流,从t=0开始,磁感应强度B随时间t变化的示意图为( )


套在长绝缘直棒上的小环质量为 ,带电量为
,带电量为 ,小环内径比棒的直径略大。将棒放置在方向均水平且正交的匀强电场和匀强磁场中,电场强度为E,磁感应强度为B,小环与棒的动摩擦因数为
,小环内径比棒的直径略大。将棒放置在方向均水平且正交的匀强电场和匀强磁场中,电场强度为E,磁感应强度为B,小环与棒的动摩擦因数为 ,重力加速度为
,重力加速度为 ,现将小环从静止释放,小环可沿绝缘直棒下滑,棒足够长,求:
,现将小环从静止释放,小环可沿绝缘直棒下滑,棒足够长,求:
(1)小环从静止释放瞬间加速度 的大小
的大小
(2)小环运动过程的最大加速度 为多大,此时速度
为多大,此时速度 为多大?
为多大?
(3)小环运动过程张最大速度 为多大?
为多大?
如图所示,固定水平桌面上的金属框架abcd,处在竖直向下的匀强磁场中,金属棒MN搁在框架上,可无摩擦滑动,此时abcd构成一个边长为L的正方形,棒的电阻为r,其余部分电阻不计,开始时磁感强度为B0.
(1)若从t=0时刻起,磁感强度逐渐减小,当棒以恒定速度v向右作匀速运动时,可使棒中不产生感应电流,则磁感强度应怎样随时间变化(写出B与t的关系式)?
(2)若从t=0时刻起,磁感强度均匀增加,每秒增量为k,同时保持棒静止,求棒中的感应电流和方向.
如图所示,匀强磁场垂直于矩形线框abcd,磁场的磁感应强度为B,矩形面积为S,现使矩形线框以ab边为轴转动90°,则在这个过程中,穿过线框的磁通量变化量是
| A.0 | B. |
C.BS | D.2BS |
如图所示,绝缘轨道由弧形轨道和半径为R=0.16m的圆形轨道、水平轨道连接而成,处于竖直面内的匀强电场中,PQ左右两侧电场方向相反,其中左侧方向竖直向下,场强大小均为103V/m,不计一切摩擦。质量为m=0.1kg的带正电小球可看作质点)从弧形轨道某处由静止释放,恰好能通过圆形轨道最高点,小球带电荷量q="1." 0×10-3C,g取10m/s2。求: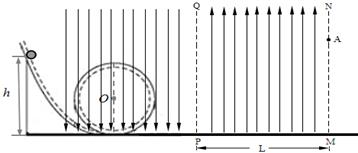
(1)小球释放点的高度h
(2)若PQ右侧某一区域存在垂直纸面向里的匀强磁场(图中未画出),磁感应强度B=4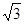 ×102T,小球通过圆形轨道后沿水平轨道运动到P点进入磁场,从竖直边界MN上的A点离开时速度方向与电场方向成30o,已知PQ、MN边界相距L=0.7m,求:
×102T,小球通过圆形轨道后沿水平轨道运动到P点进入磁场,从竖直边界MN上的A点离开时速度方向与电场方向成30o,已知PQ、MN边界相距L=0.7m,求:
①小球从P到A经历的时间
②若满足条件的磁场区域为一矩形,求最小的矩形面积。
如图所示,ABC为与匀强磁场垂直的边长为a的等边三角形,比荷为e/m的电子以速度v0从A 点沿AB边入射,欲使电子经过BC边,磁感应强度B的取值为( )

A.B> |
B.B< |
C.B> |
D.B< |
下列说法正确的是
| A.穿过线圈的磁通量越大,产生的感应电动势越大 |
| B.穿过线圈的磁通量为零,产生的感应电动势为零 |
| C.穿过线圈的磁通量变化越大,产生的感应电动势越大 |
| D.穿过线圈的磁通量变化率越大,产生的感应电动势越大 |
根据磁感应强度的定义式 ,下列说法正确的是( )
,下列说法正确的是( )
| A.在磁场中某确定位置,B与F成正比,与I、L的乘积成反比 |
| B.一小段通电直导线在空间某处受磁场力F=0,那么该处的B一定为零 |
| C.磁场中某处的B的方向跟电流在该处受磁场力F的方向相同 |
| D.一小段通电直导线放在B为零的位置,那么它受到的磁场力F也一定为零 |
目前有一种磁强计,用于测定地磁场的磁感应强度.磁强计的原理如图所示,电路有一段金属导体,它的横截面是宽为A.高为b的长方形,放在沿y轴正方向的匀强磁场中,导体中通有沿x轴正方向、大小为I的电流.已知金属导体单位体积中的自由电子数为n,电子电荷量为e,金属导电过程中,自由电子所做的定向移动可视为匀速运动.两电极M、N均与金属导体的前后两侧接触,用电压表测出金属导体前后两个侧面间的电势差为U.则磁感应强度的大小和电极M、N的正负为( )

A.,M正、N负 B.,M正、N负
C.,M负、N正 D.,M负、N正
如图所示,三根彼此绝缘的无限长直导线的一部分 、
、 、
、 构成一个等边三角形,O为三角形的中心,M、N分别为O关于导线
构成一个等边三角形,O为三角形的中心,M、N分别为O关于导线 、
、 的对称点,当三根导线中通以大小相等,方向如图所示的电流时,M点磁感应强度的大小为
的对称点,当三根导线中通以大小相等,方向如图所示的电流时,M点磁感应强度的大小为 ,O点磁感应强度的大小为
,O点磁感应强度的大小为 ,若将导线
,若将导线 中的电流撤去,而保持另两根导线中的电流不变,则N点磁感应强度的大小为( )
中的电流撤去,而保持另两根导线中的电流不变,则N点磁感应强度的大小为( )

A. |
B. |
C. |
D. |
如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间。通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则
| A.Φ1=Φ2 | B.Φ1>Φ2 | C.Φ1>Φ3 | D.Φ3>Φ2 |