高中物理磁感应强度试题

如图所示，真空中狭长区域内的匀强磁场的磁感应强度为B，方向垂直纸面向里，区域宽度为d，边界为CD和EF，速度为v的电子从边界CD外侧沿垂直于磁场方向射入磁场，入射方向跟CD的夹角为θ，已知电子的质量为m、带电荷量为e，为使电子能从另一边界EF射出，电子的速率应满足的条件是（   ）

A．

B．

C．

D．

下列可用来表示磁感应强度的单位关系的是（     ）

A．1T=1kg/m^2	B．1T=1kg/（）
C．1T=1kg/（）	D．1T=1N/（）

如图所示的天平可用来测定磁感应强度，天平的右臂下面挂有一个矩形线圈，宽为L，共N匝，线圈下部悬在匀强磁场中，磁场方向垂直纸面，当线圈中通有电流I时，方向如图，在天平左右两盘各加质量分别为m₁、m₂的砝码，天平平衡，当电流反向时（大小不变)，右盘再加上质量为m的砝码后，天平重新平衡,试求（g=10m/s²）：

（1)判定磁场的方向并推导磁感应强度的表达式
（2)当L=0.1m； N=10； I=0.1A；m=9×10^-3kg时磁感应强度是多少？

关于磁场，下列说法错误的是（     ）

A．磁感应强度B是反映磁场强弱的物理量

B．由可知，B与F成正比，与IL成反比

C．地磁场北极在地理南极附近，二者不是重合的

D．电流与电流，磁极与磁极，磁极与电流之间都是通过磁场发生作用力的

如图所示，在倾角为37°的固定金属导轨上，放置一个长L=0.4m、质量m=0.3kg的导体棒，导体棒垂直导轨且接触良好。导体棒与导轨间的动摩擦因数μ=0.5。金属导轨的一端接有电动势E＝4.5V、内阻r＝0.50Ω的直流电源，电阻R＝2.5Ω，其余电阻不计，假设最大静摩擦力等于滑动摩擦力。现外加一与导体棒垂直的匀强磁场，（sin37°=0.6，cos37°=0.8  g=10m/s²）求：

（1）使导体棒静止在斜面上且对斜面无压力，所加磁场的磁感应强度B的大小和方向；
（2）使导体棒静止在斜面上，所加磁场的磁感应强度B的最小值和方向。

三根平行的长直通电导线，分别通过一个等腰直角三角形的三个顶点且与三角形所在平面垂直，如图所示，现在使每根通电导线在斜边中点O处所产生的磁感应强度大小均为B，则下列说法中正确的有（  ）

A．O点处实际磁感应强度的大小为B

B．O点处实际磁感应强度的大小为B

C．O点处实际磁感应强度的方向与斜边夹角为90°

D．O点处实际磁感应强度的方向与斜边夹角正切值为2

如图，在xOy平面中有一通电直导线与Ox、Oy轴相交，导线中电流方向如图所示。该区域有匀强磁场，通电直导线所受磁场力的方向与Oz轴的正方向相同。该磁场的磁感应强度的方向可能是

A．沿x轴正方向	B．沿y轴负方向
C．沿z轴正方向	D．沿z轴负方向

关于磁感应强度的单位，下列等式中哪些单位是正确的

A．1特斯拉＝1千克·安培／秒^2	B．1特斯拉＝1千克／安培秒^2
C．1特斯拉＝l安培／千克秒	D．1特斯拉＝1安培·秒^2／千克

如右图所示，在矩形ABCD区域内，对角钱BD以上的区域存在有平行于AD向下的匀强电场，对角线BD以下的区域存在有垂直于纸面的匀强磁场（图中未标出），矩形AD边长L，AB边长为2L。一个质量为m、电荷量为+q的带电粒子（重力不计）以初速度v_o从A点沿AB方向进入电场，在对角线BD的中点P处进入磁场，并从DC边上以垂直于DC边的速度离开磁场（图中未画出），求：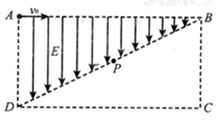

（1）电场强度E的大小
（2）带电粒子经过P点时速度v的大小和方向：
（3）磁场的磁感应强度B的大小和方向。

如图所示，一个质量为m、电荷量为＋q的圆环，可在水平放置的足够长的粗糙细杆上滑动，细杆处在磁感应强度为B的匀强磁场中(不计空气阻力)．现给圆环向右的初速度v₀，在以后的运动过程中，圆环运动的速度图象可能是图中的

一平面线圈用细杆悬于P点，开始时细杆处于水平位置，释放后让它在如图所示的匀强磁场中运动.已知线圈平面始终与纸面垂直，当线圈第一次通过位置B和位置C的过程中，下列对磁通量变化判断正确的是

A．一直变大	B．一直变小
C．先变大后变小	D．先变小后变大

磁感应强度的单位是特斯拉(T)，与它等价的是

A．

B．

C．

D．

在通电螺线管内部有一点A，通过A点的磁感线方向一定是（ ）

A．从螺线管的N极指向S极

B．放在该点的小磁针北极受力的方向

C．从螺线管的S极指向N极

D．放在该点的小磁针的南极受力的方向

下列说法中正确的是                                               （    ）

A．由B=F/IL可知，磁感应强度B与一小段通电直导线受到的磁场力成正比

B．一小段通电导线所受磁场力的方向就是磁场方向

C．一小段通电导线在某处不受磁场力，该处磁感应强度一定为零

D．磁感应强度为零的地方，一小段通电导线在该处不受磁场力

如图所示，垂直于纸面向里的匀强磁场有明显的圆形边界，圆心为O，半径为R，磁感应强度为B，现在在纸面内放上圆线圈，圆心在O处，半径为r（r<R），共有N匝。求：穿过这个线圈的磁通量。