高中物理焦耳定律试题

如图甲所示，左侧接有定值电阻的水平粗糙导轨处于垂直纸面向外的匀强磁场中，磁感应强度B=1T，导轨间距L=lm。一质量m=2kg，阻值的金属棒在水平拉力F作用下由静止开始从CD处沿导轨向右加速运动，金属棒的v—x图像如图乙所示，若金属棒与导轨间动摩擦因数，则从起点发生x=1m位移的过程中(g=10m／s²)

A．金属棒克服安培力做的功W1="0" 5J

B．金属棒克服摩擦力做的功W2=4J

C．整个系统产生的总热量Q="4" 25J

D．拉力做的功W="9" 25J

有一玩具起重机的直流电动机如图所示，已知电源电动势，电源内阻，电阻，电动机的内阻，当电动机正常工作时，电压表的示数为。求：

（1）电动机正常工作时电流表的示数；
（2）电动机正常工作时的输出功率。

如图甲所示的电路中，R₁、R₂均为定值电阻，且R₁＝100 Ω，R₂阻值未知，R₃为一滑动变阻器．当其滑片P从左端滑至右端时，测得电源的路端电压随电源中流过的电流变化图线如图乙所示，其中A、B两点是滑片P在变阻器的两个不同端点得到的．求：

（1）电源的电动势和内阻.
（2）定值电阻R₂的阻值．
（3）滑动变阻器的最大阻值．
（4）上述过程中R₁上得到的最大功率以及电源的最大输出功率。

如图为某种电磁泵模型，泵体是长为L₁，宽与高均为L₂的长方体。泵体处在方向垂直向外、磁感应强度为B的匀强磁场中，泵体的上下表面接电压为U的电源(内阻不计)，理想电流表示数为I，若电磁泵和水面高度差为h，液体的电阻率为ρ，在t时间内抽取液体的质量为m，不计液体在流动中和管壁之间的阻力，取重力加速度为g。则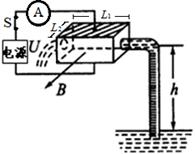

A．泵体上表面应接电源负极

B．电磁泵对液体产生的推力大小为BIL1

C．电源提供的电功率为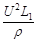

D．质量为m的液体离开泵时的动能为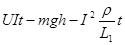

在如图甲所示的电路中，L₁、L₂和L₃为三个相同规格的小灯泡，这种小灯泡的伏安特性曲线如图乙所示，当开关S闭合后，电路中的总电流为0.25A．则此时（ ）

A．L₁的电压为L₂电压的2倍
B．L₁消耗的电功率为0.75W
C．L₂的电阻为12Ω
D．L₁、L₂消耗的电功率的比值大于4：1

如图所示，边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场，一个边长为l的正方形金属导线框所在平面与磁场方向垂直，导线框和虚线框的对角线共线，每条边的材料均相同。从t＝0开始，使导线框从图示位置开始以恒定速度沿对角线方向进入磁场，直到整个导线框离开磁场区域。导线框中的感应电流i(取逆时针方向为正)、导线框受到的安培力F(取向左为正)、导线框中电功率的瞬时值P以及通过导体横截面的电荷量q随时间变化的关系正确的是  

如图所示，R为电阻箱，V为理想电压表。闭合开关，当电阻箱读数为R₁=2Ω时，电压表读数为U₁=4V；当电阻箱读数为R₂=5Ω时，电压表读数为U₂=5V，求：

(1)电源的电动势E和内阻r
(2)当电阻箱R读数为多少时，电源的输出功率最大？最大值P_m为多少？

灵巧、省力的电动自行车，最近几年已成为人们出行的主要交通公具。下表为一辆电动自行车的铭牌上给出的技术参数。请利用表中数据进行计算：（取g=10m/s²）

规  格	后轮驱动直流电机
车型	26英寸	额定输出功率	160W
整车质量	40kg	额定电压	40V
最大载量	120kg	额定电流	5.0A

 
（1）电动机以额定值正常工作时的机械效率。
（2）在额定电压下，电机突然卡死时，电机的总功率。
（3）当自行车以额定功率在平直公路上满载匀速行驶时，若其受到的阻力为总重量的0.02倍，则此时其速度为多少？

如图甲所示，一个圆形线圈的匝数n＝100，线圈面积S＝200 cm²，线圈的电阻r＝1 Ω，线圈外接一个阻值R＝4 Ω的电阻，把线圈放入一方向垂直线圈平面向里的匀强磁场中，磁感应强度随时间变化规律如图乙所示。下列说法中正确的是

A．线圈中的感应电流方向为顺时针方向

B．电阻R两端的电压随时间均匀增大

C．前4 s内通过R的电荷量为4×10^－4 C

D．线圈电阻r消耗的功率为4×10^－4 W

用电动势为E、内电阻为r的电池组直接向线圈电阻为R的电动机供电，电动机正常工作后，测得通过的电流为l、电动机两端的电压为U，则

A．电路中电流

B．在时间t内，电池组消耗的化学能为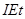

C．在时间t内，电动机输出的机械能是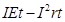

D．以上说法都不对

一理想变压器的原、副线圈的匝数比为3:1，在原、副线圈的回路中分别接有阻值相同的电阻，原线圈一侧接在电压为的正弦交流电源上，如图所示。设副线圈回路中电阻两端的电压为，原、副线圈回路中电阻消耗的功率的比值为，则（）

A．		B．
C．		D．

真空中放置的平行金属板可以用作光电转换装置，如图所示，光照前两板都不带电，以光照射板，则板中的电子可能吸收光的能量而逸出。假设所有逸出的电子都垂直于板向板运动，忽略电子之间的相互作用，保持光照条件不变，为接线柱。已知单位时间内从板逸出的电子数为，电子逸出时的最大动能为，元电荷为。

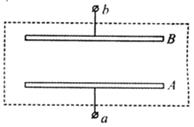
（1）求板和板之间的最大电势差，以及将短接时回路中的电流。
（2）图示装置可看作直流电源，求其电动势和内阻.
（3）在之间连接一个外电阻时，该电阻两端的电压为，外电阻上消耗的电功率设为;单位时间内到达板的电子，在从板运动到板的过程中损失的动能之和设为，请推导证明：.( 注意：解题过程中需要用到、但题目没有给出的物理量，要在解题中做必要的说明)

如图所示，R₁为定值电阻，R₂为可变电阻，E为电源电动势，r为电源的内电阻，以下说法中不正确的是

A．当R2=Rl + r时，R2上获得最大功率

B．当Rl=R2 + r时，Rl上获得最大功率

C．当R2=0时Rl上获得功率一定最大

D．当R2=0时，电源的输出功率可能最大

如图所示，在光滑绝缘的水平面上方，有两个方向相反的水平方向的匀强磁场，PQ为两磁场的边界，磁场范围足够大，磁感应强度的大小分别为B₁＝B，B₂＝2B，一个竖直放置的边长为a、质量为m、电阻为R的正方形金属线框，以初速度v垂直磁场方向从图中实线位置开始向右运动，当线框运动到在每个磁场中各有一半的面积时，线框的速度为v/2，则下列判断正确的是

A．此过程中通过线框截面的电量为

B．此过程中线框克服安培力做的功为mv^2

C．此时线框的加速度为

D．此时线框中的电功率为

额定电压为4.0V的直流电动机的线圈电阻为1.0，正常工作时，电动机线圈每秒产生的热量为4.0J，下列计算结果正确的是

A．电动机正常工作时的电流强度为4.0A

B．电动机正常工作时的输出功率为8.0W

C．电动机每分钟将电能转化成机械能为240.0J

D．电动机正常工作时的输入功率为4.0W