高中物理闭合电路中的能量转化计算题

如图，A、B、C三个木块的质量均为m，置于光滑的水平桌面上，B、C之间有一轻质弹簧，弹簧的两端与木块接触而不固连．将弹簧压紧到不能再压缩时用细线把B和C紧连，使弹簧不能伸展，以至于B、C可视为一个整体．现A以初速度v₀沿B、C的连线方向朝B运动，与B相碰并粘合在一起．以后细线突然断开，弹簧伸展，从而使C与A、B分离．已知离开弹簧后C的速度恰好为v₀．求弹簧释放的势能．

如图所示，为一传送装置，其中AB段粗糙，AB段长为L=0.2m，动摩擦因数，BC、DEN段均可视为光滑，且BC的始末端均水平，具有h=0.1m的高度差，DEN是半径为r=0.4m的半圆形轨道，其直径DN沿竖直方向，C位于DN竖直线上，CD间的距离恰能让小球自由通过，在左端竖直墙上固定有一轻质弹簧，现有一可视为质点的小球，小球质量m=0.2kg，压缩轻质弹簧至A点后静止释放（小球和弹簧不黏连），小球刚好能沿DEN轨道滑下，求：

（1）小球刚好能通过D点时速度的大小。
（2）小球到达N点时速度的大小及受到轨道的支持力的大小
（3）压缩的弹簧所具有的弹性势能

在光滑的水平地面上静止着一质量M＝0.4kg的薄木板，一个质量m＝0.2kg的木块(可视为质点)以v₀＝4m/s的速度，从木板左端滑上，一段时间后，又从木板上滑下(不计木块滑下时的机械能损失)，两物体仍沿直线继续向前运动，从木块与木板刚刚分离开始计时，经时间t＝3.0s，两物体之间的距离增加了s＝3m，已知木块与木板的动摩擦因数μ＝0.4，求薄木板的长度．

如图所示，质量为M=384g的木块放在光滑的水平面上，质量为m =20g的子弹以速度v₀沿水平方向射中木块,并最终停留在木块中与木块一起以速度v运动。当子弹进入木块的深度为d=0.1m时两者相对静止，这时木块前进的距离为X=0.4m，若木块对子弹的摩擦阻力大小为F_f = 48N视为恒力，试求：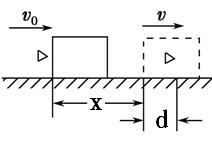

木块对子弹做的功W₁和子弹对木块做的功W₂
子弹与木块的最终速度v和子弹的初速度v₀。

如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点相切，半圆形导轨的半径为R。一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右的速度后脱离弹簧，当它经过B点进入导轨的瞬间对轨道的压力为其重力的8倍，之后向上运动恰能到达最高点C。(不计空气阻力)试求：

(1)物体在A点时弹簧的弹性势能；
(2)物体从B点运动至C点的过程中产生的内能。

某校物理兴趣小组决定举行遥控赛车比赛。比赛路径如图所示，赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直圆轨道，离开竖直圆轨道后继续在平直轨道上运动到C点，并越过壕沟。已知赛车质量m=0.1kg，通电后以额定功率P=1.4W工作，水平轨道的摩擦阻力恒为0.20N。图中L=10.0m，BC=1.5m，R=0.32m，h=1.25m，S=1.5m。重力加速度g取10m/s²。求：

（1）赛车要越过壕沟，离开C点的速度至少多大？
（2）赛车要通过光滑竖直轨道，刚进入B点时的最小速度多大？赛车的电动机在AB段至少工作多长时间？
（3）要使赛车完成比赛，赛车离开光滑竖直轨道后，电动机在BC段是否还要继续工作？（要通过计算回答）

如图所示，水平传送带在电劫机的带动下，始终保持v的速度运行。质量为m的工件（可视为质点）轻轻放在传送带上，过一会儿与传送带相对静止。对于这个过程，求：电动机由于传送工件多消耗的电能。

如图所示，质量为m=0.1kg的小球置于平台末端A点，平台的右下方有一个表面光滑的斜面体，在斜面体的右边固定一竖直挡板，轻质弹簧栓接在挡板上，弹簧的自然长度为，斜面体底端C点距挡板的水平距离为，斜面体的倾角为，斜面体的高度h=0.5m。现给小球一大小为的初速度，使之在空中运动一段时间后，恰好从斜面体的顶端B点无碰撞地进入斜面，并沿斜面运动，经过C点后再沿粗糙水平面运动，过一段时间开始压缩轻质弹簧；小球速度减为零时，弹簧被压缩了。已知小球与水平面的动摩擦因数μ=0.5，设小球经过C点时无机械能损失，重力加速度，求：

（1）平台与斜面体间的水平距离
（2）小球在斜面上的运动时间
（3）弹簧压缩过程中的最大弹性势能

水平传送带被广泛地应用于机场和火车站，用于对旅客的行李进行安全检查，右图为一水平传送带装置示意图，绷紧的传送带AB始终保持1 m/s的恒定速度运行，一质量为m="4" kg的行李无初速地放在A处，传送带对行李的滑动摩擦力使行李开始做匀加速直线运动，该行李与传送带间的动摩擦因数μ=0.1,AB间的距离l="2" m,g取10 m/s²。求:

(1)行李被从A运送到B所用时间。
(2)电动机运送该行李需增加的电能为多少？
(3)如果提高传送带的运动速率，行李就能够较快地传送到B处，求行李从A处传送到B处的最短时间和传送带对应的最小运行速率。

如图所示，光滑水平面MN的左端M处有一弹射装置P(P为左端固定，处于压缩状态且锁定的轻质弹簧，当A与P碰撞时P立即解除锁定)，右端N处与水平传送带恰平齐且很靠近，传送带沿逆时针方向以恒定速率υ =" 5m/s" 匀速转动，水平部分长度L = 4m。放在水平面上的两相同小物块A、B（均视为质点）间有一被压缩的轻质弹簧，弹性势能E_p = 4J，弹簧与A相连接，与B不连接，A、B与传送带间的动摩擦因数μ = 0.2，物块质量m_A = m_B = 1kg。现将A、B由静止开始释放，弹簧弹开，在B离开弹簧时，A未与P碰撞，B未滑上传送带。取g = 10m/s²。求：
（1）B滑上传送带后，向右运动的最远处与N点间的距离sm；
（2）B从滑上传送带到返回到N端的时间t和这一过程中B与传送带间因摩擦而产生的热 能Q；
（3）B回到水平面后压缩被弹射装置P弹回的A上的弹簧，B与弹簧分离然后再滑上传       送带。则P锁定时具有的弹性势能E满足什么条件，才能使B与弹簧分离后不再与弹簧相碰。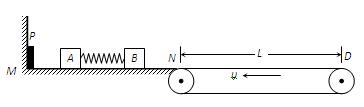

如图所示，物体在有动物皮毛的斜面上运动，由于皮毛的特殊性，引起物体的运动有如下特点，①顺着毛的生长方向运动时，毛皮产生的阻力可以忽略，②逆着毛的生长方向运动时，会受到来自毛皮的滑动摩擦力，且动摩擦因数μ恒定，斜面底端距水平面高度为h=0.8m，质量为m=2kg的小物块M从斜面顶端A由静止滑下，从O点进入光滑水平滑道时无机械能损失，为使M制动，将轻弹簧的一端固定在水平滑道延长线B处的墙上，另一端恰位于水平轨道的中点C，已知斜面的倾角，动摩擦因数均为μ=0.5，其余各处的摩擦不计，重力加速度，下滑时逆着毛的生长方向，求

（1）弹簧压缩到最短时的弹性势能（设弹簧处原长时弹性势能为零）
（2）若物块M能够被弹回到斜面上，则它能够上升的最大高度是多少
（3）物块M在斜面上滑过程中下滑的总路程

如图1所示，一根轻质弹簧左端固定在水平桌面上，右端放一个可视为质点的小物块，小物块的质量为m=1.0kg，当弹簧处于原长时，小物块静止于O点，现对小物块施加一个外力，使它缓慢移动，压缩弹簧x=0.1m至A点，在这一过程中，所用外力与弹簧压缩量的关系如图2所示．然后释放小物块，让小物块沿桌面运动，已知O点至桌边B点的距离为L=0.2m．水平桌面的高为h=1.8m，计算时，可取滑动摩擦力近似等于最大静摩擦力．（g取10m/s²）

求：（1）压缩弹簧过程中，弹簧存贮的最大弹性势能；
（2）小物块落地点与桌边B的水平距离．

如图，A、B、C三个木块的质量均为m。置于光滑的水平面上，B、C之间有一轻质弹簧，弹簧的两端与木块接触而不固连。将弹簧压紧到不能再压缩时用细线把B和C紧连，使弹簧不能伸展，以至于B、C可视为一个整体。现A以初速v₀沿B、C的连线方向朝B运动，与B相碰并粘合在一起。以后细线突然断开，弹簧伸展，从而使C与A、B分离。已知C离开弹簧后的速度恰为v₀。求弹簧释放的势能。

如图所示，光滑水平轨道左端与长L=1.25m的水平传送带AB相接，传送带逆时针匀速转动的速度，轻弹簧右端固定，弹簧处于自然状态时左端恰位于A点，现用质量m=0.1kg的小物块（视为质点）将弹簧压缩后由静止释放，到达水平传送带左端B点后，立即沿切线进入竖直固定的光滑半圆轨道最高点并恰好做圆周运动，经圆周最低点C后滑上质量为M=0.9kg的长木板且不会从木板下掉下。半圆轨道的半径R=0.4m，物块与传送带间动摩擦因数，物块与木块间动摩擦因数，长木板与水平地面间的动摩擦因数，，求：

（1）物块到达B点时的速度的大小；
（2）弹簧被压缩时的弹性势能；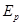
（3）小物块在长木板上滑行的最大距离s。

如图所示，质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点，水平轻质弹簧一端栓在固定挡板P上，另一端与靶盒A连接。Q处有一固定的发射器B，它可以瞄准靶盒发射一颗水平速度为v₀=50m／s，质量m=0.010kg的弹丸，当弹丸打入靶盒A后，便留在盒内，碰撞时间极短。不计空气阻力。求弹丸进入靶盒A后，弹簧的最大弹性势能为多少？