高中物理等势面计算题

如图所示，BC是半径为R的圆弧形的光滑且绝缘的轨道，位于竖直平面内，其下端与水平绝缘轨道平滑连接，整个轨道处在水平向左的匀强电场中，电场强度为E．今有一质量为m、带正电q的小滑块（体积很小可视为质点），从C点由静止释放，滑到水平轨道上的A点时速度减为零．若已知滑块与水平轨道间的动摩擦因数为μ，求：

（1）滑块通过B点时的速度大小V_b？
（2）水平轨道上A、B两点之间的距离S？

质量为m的带电小球用细绳系住悬挂于匀强电场中，如图所示，静止时θ角为60°，求：

（1）小球带何种电性．
（2）若将绳烧断后，2s末小球的速度是多大．（g取10m/s²）

在相互垂直的匀强电场和匀强磁场中，有一倾角为θ，足够长的光滑绝缘斜面，磁感应强度为B，方向垂直纸面向外，电场方向竖直向上．有一质量为m，带电量为十q的小球静止在斜面顶端，这时小球对斜面的正压力恰好为零，如图所示，若迅速把电场方向反转竖直向下，小球能在斜面上连续滑行多远？所用时间是多少？

如图甲所示，M、N为水平放置的平行板电容器的两个极板，极板长L="0.2" m，两板间距d=0.1m，在从M、N间加上如图乙所示的电压，一个带电粒子的电量q=+l.0×10^-6C、质量m=1.0×10^-8kg，粒子重力不计，求：

（1）0～1×10^-3s电容器内部场强的大小和方向；
（2）若在t=0的时刻，将上述带电粒子从紧靠M板中心处无初速释放，求粒子从M板运动到N板所经历的时间t；
（3）若在t=0的时刻，上述带电粒子从靠近M板的左边缘处以初速度v₀水平射入两极板间，且粒子沿水平方向离开电场，求初速度v₀的大小。

如图，光滑绝缘半球槽的半径为R，处在水平向右的匀强电场中，一质量为m的带电小球从槽的右端A处无初速沿轨道滑下，滑到最低点B时，球对轨道的压力为2mg。求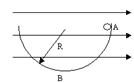


（1）小球受到的电场力的大小和方向。
（2）带电小球在滑动过程中的最大速度。

如图所示，质量m=5.0×10^-8kg的带电粒子，以初速v₀=2m/s的速度从水平放置的平行金属板A、B的中央，水平飞入电场，已知金属板长0.1m，板间距离d=2×10^-2m，当U_AB=1000V时，带电粒子恰好沿直线穿过电场，若两极板间的电势差可调，要使粒子能从两板间飞出，U_AB的变化范围是多少?（g取10m/s²）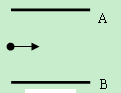

电路如图所示，电源电动势E＝28 V，内阻r＝2 Ω，电阻R₁＝12 Ω，R₂＝R₄＝4Ω，R₃＝8Ω，C为平行板电容器，其电容C＝3.0 pF，虚线到两极板距离相等，极板长l＝0.20 m，两极板的间距d＝1.0×10^－2 m。

(1)若开关S处于断开状态，则当其闭合后，求流过R₄的总电量为多少？
(2)若开关S断开时，有一带电微粒沿虚线方向以v₀＝2.0 m/s的初速度射入C的电场中，刚好沿虚线匀速运动，问：当开关S闭合后，此带电微粒以相同初速度沿虚线方向射入C的电场中，能否从C的电场中射出？(要求写出计算和分析过程，g取10m/s²)

如图所示，在xOy坐标平面中，有正方形区域abcd，其中的两条边界与坐标轴重合，区域内有竖直向上的匀强电场，电场强度为E。质量为m、电量为q的带电粒子，不计重力，由初速度为零经加速电场后获得速度，并从坐标原点沿x正方向进入电场，恰好从c点飞出电场。

（1）求加速电压
（2）求ac两点间的电势差；
（3）推导证明：带电粒子在正方形区域内运动过程中，动能与电势能之和不变。

如下图甲所示，在y＝0和y＝3m之间有沿着x轴方向的匀强电场，MN为电场区域的上边界，在x轴方向范围足够大．电场强度的变化如图乙所示，取x轴正方向为电场正方向，现有一个带正电的粒子，粒子的比荷为，在t＝0时刻以速度v₀＝5×10²m/s从O点沿y轴正方向进入电场区域，不计粒子重力，求：

（1）粒子通过电场区域的时间；
（2）粒子离开电场时的位置坐标；
（3）粒子刚通过电场区域时速度方向与x轴正方向夹角的正切值（保留3位有效数字）．

一电路如图所示，电源电动势E=28V，内阻r=2Ω，电阻R₁=12Ω，R₂=4Ω，R₃=8Ω，C为平行板电容器，其电容C ="3.0" pF，虚线到两极板距离相等，极板长L=0.20m，两极板的间距d=1.0×10^-2m。

（1）开关S处于断开状态时电容器所带电量为多少？
（2）若开关S断开时，有一带电微粒沿虚线方向以的初速度射入C的电场中，刚好沿虚线匀速运动，问：当开关S闭合后，此带电微粒以相同初速度沿虚线方向射入C的电场中，能否从C的电场中射出？（要求写出计算和分析过程，g取10m/s²）

如图所示，在竖直向下的匀强电场中有一绝缘的光滑轨道，一个带负电的小球从斜轨上的A点由静止释放，沿轨道滑下，已知小球的质量为m，电荷量为－q，匀强电场的场强大小为E，斜轨道的倾角为α，圆轨道半径为R，小球的重力大于所受的电场力．

(1)求小球沿轨道滑下的加速度的大小；
(2)若小球能通过圆轨道顶端的B点，求A点距水平地面的高度h至少为多大。

如图所示，水平放置的平行板电容器，与某一电源相连．它的极板长L=0.4m，两板间距离d=4×10^﹣3m，有一束由相同带电微粒组成的粒子流，以相同的速度v₀从两板中央平行极板射入，开关S闭合前，两板不带电，由于重力作用微粒能落到下板的正中央，已知微粒质量为m=4×10^﹣5kg，电量q=+1×10^﹣8C，（g=10m/s²）求：

（1）微粒入射速度v₀为多少？
（2）为使微粒能从平行板电容器的右边射出电场，电容器的上板应与电源的正极还是负极相连？所加的电压U应取什么范围？

如图所示，匀强电场方向与水平方向的夹角θ=30°斜右上方，电场强度为E，质量为m的带负电的小球以初速度v₀开始运动，初速度方向与电场方向一致，试求：

（1）若小球带的电荷量为q=，为使小球能做匀速直线运动，应对小球施加的恒力F₁的大小和方向如何？
（2）若小球带的电荷量为q=，为使小球能做直线运动，应对小球施加的最小恒力F₂的大小和方向如何？

如图所示，一带电平行板电容器与水平方向成37°放置，下方有绝缘挡板支撑，板间距d=2.88cm，一带正电的小球的质量为0.02g，电荷量为10^﹣7C，由电容器的中心A点静止释放恰好沿水平直线AB向右运动，从上极板边缘飞出进入边界BC右侧的水平向左的匀强电场区域，场强为2×l0³V/m，经过一段时间后发现小球打在竖直挡板C点正下方的D处，（取g=10m/s²）求：

（1）平行板电容器内的场强大小
（2）小球从上极板边缘飞出的速度
（3）CD间的距离．

如图甲所示，两个平行正对的水平金属板XX′极板长L = 0.2m，板间距离d = 0.2m，在金属板右端竖直边界MN的右侧有一区域足够大的匀强磁场，磁感应强度，方向垂直纸面向里。现将X′极板接地，X极板上电势φ随时间变化规律如图乙所示。现有带正电的粒子流以的速度沿水平中线OO′连续射入电场中，粒子的比荷，重力可忽略不计，在每个粒子通过电场的极短时间内，电场可视为匀强电场（设两板外无电场）。求：

（1）带电粒子射出电场时的最大速率；
（2）粒子在磁场中运动的最长时间和最短时间之比；
（3）分别从O′点和距O′点下方＝0.05m处射入磁场的两个粒子，在MN上射出磁场时两出射点之间的距离。