两个相同的带异种电荷的金属小球(视为点电荷),带电量大小之比为1:5,当它们相距r时的相互作用力为F1.若把它们互相接触后再放回原处,它们的相互作用力变为F2,则F1:F2可能为( )
| A.5:1 | B.4:5 | C.5:4 | D.5:8 |
真空中两个同性的点电荷q1、q2,它们相距较近,保持静止。今释放q2且q2只在q1的库仑力作用下运动,则q2在运动过程中受到的库仑力( )
| A.先增大后减小 | B.不断增加 | C.始终保持不变 | D.不断减小 |
自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们距离的二次方成反比。发现此定律的科学家是 。 (2)在真空中两点电荷,相隔距离为r时的库仑力大小为F,若保持这两个点电荷的电荷量不变,当它们距离为0.2r时相互作用力为 F。
对于库仑定律,下面说法正确的是( )
| A.库仑定律是实验定律 |
| B.两个带电小球即使相距非常近,也能直接用库仑定律 |
| C.相互作用的两个点电荷,不论它们的电荷量是否相同,它们之间的库仑力大小一定相等 |
| D.根据库仑定律,当两个带电体的距离趋近于零时,库仑力趋近于无穷大 |
如图所示,竖直绝缘墙壁上的Q处有一固定的质点A,在Q的正上方的P点用丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,致使悬线与竖直方向成θ角,由于漏电使A、B两质点的电荷量逐渐减少,在电荷漏电完毕之前悬线对悬点P的拉力大小

A. 不变 B.变大 C. 变小 D.无法确定
在电磁学发展过程中,科学家们做出了很大贡献。下列说法符合事实的是
| A.焦耳发现了焦耳定律;亨利发现了自感现象 |
| B.奥斯特发现了电流磁效应;洛仑兹发现了磁场对电流的作用规律 |
| C.安培最早引入了电场概念;楞次发现了楞次定律 |
| D.库仑发现了点电荷的相互作用规律;密立根通过油滴实验测定了元电荷的数值 |
A、B两个带同种电荷的绝缘金属小球,半径为r,球心相距3r,A带电荷量Q1,B带电荷量Q2,则A、B间相互作用力 ( )
A.无法确定 B.等于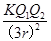
C.大于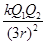 D.小于
D.小于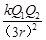
如图所示,倾角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过绝缘细绳跨过光滑的定滑轮与带正电小球M连接,连接b的一段细绳与斜面平行,带负电的小球N固定在M的正下方。两带电小球在缓慢漏电的过程中,M、b、c都处于静止状态,下列说法中正确的是( )
| A.b对c的摩擦力可能始终增加 |
| B.地面对c的支撑力始终变小 |
| C.c对地面的摩擦力方向始终向左 |
| D.滑轮对绳的作用力方向始终不变 |
如图所示,两个等量异号的点电荷在其连线的中垂线上有与连线中点O等距离的两点a、b,在连线上有距中点O等距离的两点c、d,则下列场强大小关系式正确的是( )
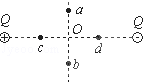
| A.Ea=Eb<Ec | B.Ea=EO=Eb | C.Ea<Ed | D.Ec>EO>Ed |
已知点电荷A的电荷量是点电荷B的2倍,则A对B的作用力大小跟B对A的作用力大小的比值为( )
| A.2∶1 | B.1∶2 | C.1∶1 | D.不能确定 |
假设两个带异种电荷的小球放在光滑绝缘的水平桌面上,由静止释放,在两小球碰撞之前,两球的( )
| A.加速度逐渐变小 库仑力逐渐变大 |
| B.速度逐渐变大 库仑力逐渐变小 |
| C.速度逐渐变小 库仑力逐渐变小 |
| D.加速度逐渐变大,库仑力逐渐变大 |
用两根等长的细线各悬一个小球,并挂于同一点,已知两球质量相等,当它们带上同种电荷时,相距L而平衡,如图所示.若使它们的带电量都减少一半,待它们重新平衡后,两球间距离
| A.大于L/2 | B.等于L/2 | C.小于L/2 | D.等于L |
如图所示在光滑、绝缘的水平面上,沿一直线依次排列三个带电小球A、B、C(可视为质点).若它们恰能处于平衡状态.那么这三个小球所带的电荷量及电性的关系,下面的情况可能的是 ( )
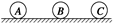
A.-9、4、-36 B.4、9、36 C.-3、2、8 D.3、-2、6
类比法是物理学重要的研究方法,比如可以将静电力与重力进行类比,以下几组物理量的类比中合理的是( )
| A.电势能与机械能 | B.电势差与高度差 |
| C.电场强度与重力 | D.电势与重力加速度 |