高中物理电荷守恒定律计算题

如图所示，光滑水平面上有一辆质量为Ｍ=1kg的小车，小车的上表面有一个质量为m=0.9kg的滑块，在滑块与小车的挡板间用轻弹簧相连接，滑块与小车上表面间的动摩擦因数为μ=0.2，整个系统一起以v₁=10m/s的速度向右做匀速直线运动，此时弹簧长度恰好为原长。现在用一质量为m₀=0.1kg的子弹，以v₀=50m/s的速度向左射入滑块且不穿出，所用时间极短。当弹簧压缩到最短时，弹簧被锁定，测得此时弹簧的压缩量为d=0.50m，g =10m/s²。求

①子弹射入滑块的瞬间，子弹与滑块的共同速度；
②弹簧压缩到最短时，弹簧弹性势能的大小。

如图所示,固定的凹槽水平表面光滑,其内放置U形滑板N,滑板两端为半径R="0.45" m
的1/4圆弧面,A和D分别是圆弧的端点,BC段表面粗糙,其余段表面光滑,小滑块P₁和P₂的质量均为m,滑板的质量M=4m.P₁和P₂与BC面的动摩擦因数分别为μ₁=0.10和μ₂=0.40,最大静摩擦力近似等于滑动摩擦力,开始时滑板紧靠槽的左端,P₂静止在粗糙面的B点。P₁以v₀="4.0" m/s的初速度从A点沿弧面自由滑下,与P₂发生弹性碰撞后,P₁停在粗糙面B点上,当P₂滑到C点时,滑板恰好与槽的右端碰撞并与槽牢固粘连,P₂继续滑动,到达D点时速度为零,P₁与P₂可视为质点,取g="10" m/s²。问：

（1）P₂在BC段向右滑动时,滑板的加速度为多大？
（2）BC长度为多少？N、P₁和P₂最终静止后,P₁与P₂间的距离为多少？

如图所示，质量为m的小球悬挂在长为L的细线下端，将它拉至与竖直方向成θ=60°的位置后自由释放．当小球摆至最低点时，恰好与水平面上原来静止的、质量为2m的木块相碰，碰后小球速度反向且动能是碰前动能的．已知木块与地面的动摩擦因素μ=，重力加速度取g．求：

（1）小球与木块碰前瞬间所受拉力大小
（2）木块在水平地面上滑行的距离

如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为m_A、m_B、m_C，且；m_A=m_B =" 1.Okg" ,m_c = 2.O kg,其中B与C用一个轻弹簧拴接在一起，开始时整个装置处于静止状态.A和B之间有少许塑胶炸药，A的左边有一个弹性挡板.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B，并且与B发生碰撞后粘在一起.忽略小木块和弹性挡板碰撞过程中的能量损失.求：

(1) 塑胶炸药爆炸后瞬间A与B的速度各为多大？
(2) 在A追上B之前弹簧弹性势能的最大值；
(3) A与B相碰以后弹簧弹性势能的最大值.

如果质点所受的力与它偏离平衡位置位移的大小成正比，并且总是指向平衡位置，即F=-kx，其中k是由系统本身特性决定的线性回复力常数，那么质点的运动就是简谐运动。

（1）图1所示为一理想单摆，摆球的质量为m，摆长为L。重力加速度为g。请通过计算说明该单摆做简谐运动的线性回复力常数k=?
（2）单摆做简谐运动的过程中，由于偏角很小，因此可以认为摆球沿水平直线运动。
如图2所示，质量为m的摆球在回复力F=-kx作用下沿水平的x轴做简谐运动，若振幅为A，在平衡位置O点的速度为v_m，试证明：。
（3）如图3所示，两个相同的理想单摆均悬挂在P点。将B球向左拉开很小的一段距离由静止释放，B球沿水平的x轴运动，在平衡位置O点与静止的C球发生对心碰撞，碰撞后B、C粘在一起向右运动。已知摆球的质量为m，摆长为L。释放B球时的位置到O点的距离为d。重力加速度为g。求B、C碰撞后它们沿x轴正方向运动的最大距离。

(1)研究发现两个氘核(H)可聚变成He，已知氘核的质量为2.013 6 u，中子的质量为1.008 7 u， He核质量为3.015 0 u．若质量亏损1 u对应的核能为931.5 MeV，则两个氘核聚变成He核的核反应方程为________________；上述反应中释放的核能为________．
(2)如图所示，光滑水平面上三个物块A、B、C，A、B间有压缩且被锁定的轻弹簧，三物块均处于静止状态．现解除对弹簧的锁定，B离开弹簧后，以速度v₀与C相碰，最终B与A运动的速度相同，已知m_A＝6 kg，m_B＝1 kg，m_C＝14 kg，求B与C相碰后C的速度大小．

（选修3-5）
（I）下列说法正确的是__________

A．放射性元素的半衰期是针对大量原子核的统计规律

B．α、β、γ射线比较，α射线的电离作用最弱

C．光的波长越短，光子的能量越大，光的粒子性越明显

D．核聚变原理是制造原子弹的理论基础

E．原子的全部正电荷和全部质量都集中在原子核里
F．由玻尔的原子模型可以推知，氢原子处于激发态，量子数越大，核外电子动能
越小
（II）如图所示，一轻质弹簧的一端固定在滑块B上，另一端与滑块C接触但未连接，该整体静置在光滑水平面上。现有一滑块A从光滑曲面上离水平面高处由静止开始滑下，与滑块B发生碰撞（时间极短）并粘在一起压缩弹簧推动滑块C向前运动，经过一段时间，滑块C脱离弹簧，继续在水平面上做匀速运动。已知,求：
（1）滑块A与滑块B碰撞时的速度大小；
（2）滑块A与滑块B碰撞结束瞬间它们的速度的大小；
（3）滑块C在水平面上匀速运动的速度的大小。

如图所示，固定的光滑圆弧面与质量为6 kg的小车C的上表面平滑相接，在圆弧面上有一个质量为2 kg的滑块A，在小车C的左端有一个质量为2 kg的滑块B，滑块A与B均可看做质点．现使滑块A从距小车的上表面高h＝1.25 m处由静止下滑，与B碰撞后瞬间粘合在一起共同运动，最终没有从小车C上滑出．已知滑块A、B与小车C的动摩擦因数均为μ＝0.5，小车C与水平地面的摩擦忽略不计，取g＝10 m/s².求：

(1)滑块A与B碰撞后瞬间的共同速度的大小；
(2)小车C上表面的最短长度．

如图，倾角为θ的斜面固定。有n个质量都为m的相同的小木块（可视为质点）放置在斜面上。相邻两小木块间距离都为，最下端的木块距底端也是，小木块与斜面间的动摩擦因数都为μ。在开始时刻，第一个小木块从斜面顶端以初速度v₀沿斜面下滑，其余所有木块都静止，由于第一个木块的下滑将依次引起一系列的碰撞。设每次碰撞的时间极短，在每次碰撞后，发生碰撞的木块都粘在一起运动，直到最后第n个木块到达底端时，速度刚好为零。已知重力加速度为g．求：

第一次碰撞后小木块1的速度大小v；
从第一个小木块开始运动到第一次碰撞后系统损失的机械能；
发生一系列碰撞后，直到最后第n个木块到达底端，在整个过程中，由于碰撞所损失的总机械能_总。

图中滑块和小球的质量均为m，滑块可在水平放置的光滑固定导轨上自由滑动，小球与滑块上的悬点O由一不可伸长的轻绳相连，轻绳长为．开始时，轻绳处于水平拉直状态，小球和滑块均静止．现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有粘住物质的固定挡板粘住，在极短的时间内速度减为零，小球继续向左摆动，当轻绳与竖直方向的夹角θ＝60°时小球到达最高点．求
（1）小球到达最低点时速度的大小；
（2）滑块与挡板刚接触的瞬时，滑块速度的大小；
（3）小球从释放到第一次到达最低点的过程中，绳的拉力对小球所做的功．

质量均为m=2kg的三物块A、B、C，物块A、B用轻弹相连，初始时弹簧处于原长，A、B两物块都以v=3m/s的速度在光滑的水平地面上运动，物块C静止在前方，如图所示。B与C碰撞后二者会粘在起运动。求在以后的运动中：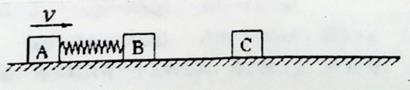

（1）从开始到弹簧的弹性势能第一次达到最大时弹簧对物块A的冲量；
（2）系统中弹性势能的最大值E_P是多少?

如图所示，一轻质弹簧两端连着物体A和B，放在光滑的水平面上，物体A被水平速度为v₀的子弹击中，子弹嵌在其中，已知A的质量是B的质量的3/4，子弹的质量是B的质量的1/4。求：

⑴A物体获得的最大速度；
⑵弹簧压缩量最大时B物体的速度。

如图所示，光滑水平面上静止放着长L=1.6m，质量为M=3kg的木块（厚度不计），一个质量为m=1kg的小物体放在木板的最右端，m和M之间的动摩擦因数μ=0.1，今对木板施加一水平向右的拉力F，（g取10m/s²）

为使小物体不掉下去，F不能超过多少？
如果F=10N，求小物体所能获得的最大动能？
如果F=10N，要使小物体从木板上掉下去，F作用的时间不能小于多少？

如图所示，水平地面上静止放置着物块B和C，相距l=1.0m。物块A以速度v₀=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动，并再与C发生正碰，碰后瞬间C的速度v=2.0m/s。已知A和B的质量均为，C的质量为A质量的K倍，物块与地面的动摩擦因数μ=0.45。（设碰撞时间很短，取10m/s²）

计算与C碰撞前瞬间AB的速度；
根据AB与C的碰撞过程分析K的取值范围，并讨论与C碰撞后AB的可能运动方向。

如图所示 ，粗糙斜面与光滑水平地面通过光滑小圆弧平滑连接，斜面倾角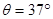，滑块A、C、D的质量均为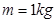，滑块B的质量为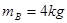，各滑块均可视为质点。A、B间夹着微量火药。K为处于原长的轻质弹簧，两端分别栓接滑块B和C。火药爆炸后，A与D相碰并粘在一起，沿斜面前进L =" 0.8" m 时速度减为零，接着使其保持静止。已知滑块A、D与斜面间的动摩擦因数均为 μ = 0.5，运动过程中弹簧始终处于弹性限度内，取 g = 10 m/s²，sin37°= 0.6，cos37°= 0.8。求：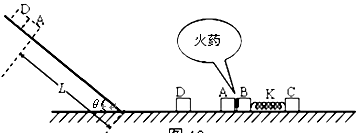

火药爆炸后A的最大速度v_A；
滑块B、C和弹簧K构成的系统在相互作用过程中，弹簧的最大弹性势能E_p；
滑块C运动的最大速度v_C。