高中物理理想气体的状态方程计算题

如图所示，一水平放置的气缸，由截面积不同的两圆筒连接而成，活塞A、B用一长为3L的刚性细杆连接，它们可以在筒内无摩擦地沿水平方向左右滑动．A、B的截面积分别为S_A=2S₀、S_B= S₀。A、B之间封闭着一定质量的理想气体．两活塞外侧（A的左方和B的右方）都是大气，大气压强始终保持为Po．活塞B的中心连一不能伸长的细线，细线的另一端固定在墙上，当气缸内气体温度为T₁=T₀，活塞A、B的平衡位置如图所示，此时细线中的张力为F₁= 0.2P₀S₀。（答案用已知量S₀、p₀、T₀表示）
（1）现使气缸内气体温度由初始温度T₁缓慢下降至T₂，T₂为多少时活塞开始向右移动？
（2）继续使气缸内气体温度缓慢下降至T₃，T₃为多少时活塞A刚刚右移到两圆筒连接处？
（3）活塞A移到两圆筒连接处之后，维持气体温度T₃不变，另外对B施加一个水平向左的推力，将两活塞慢慢推向左方，直到细线拉力重新变为F₁求此时的外加推力F是多大a

如图所示，一足够高的直立气缸上端开口，用一个厚度不计的活塞封闭了一段高为90cm的气柱，活塞的横截面积为0.01m²，活塞与气缸间的摩擦不计，气缸侧壁通过一个密封接口与U形管相通，密封接口离气缸底部的高度为70cm，气缸与U形管相通处气体体积忽略不计．在图示状态时气体的温度为17℃，U形管两支管水银面的高度差h₁为6cm，右支管内水银面到管口的高度为20cm，大气压强p₀＝1.0×10⁵Pa保持不变，水银的密度ρ＝13.6×10³kg/m³．求：

（1）活塞的重力；
（2）现在将U形管右支管开口端用橡皮塞（厚度不计）封住，并在活塞上添加沙粒，同时对气缸内的气体缓缓加热，让活塞高度始终不变．当气体温度升高到57⁰C时，不再加沙粒，同时停止对气体加热，这时U形管两支管内水银面的高度差h₂变为多少？（气缸内气体温度变化不影响U形管）
（3）保持上题中的沙粒质量不变，让气缸内的气体逐渐冷却，那么当气体的温度至少降为多少^oC时，U形管内的水银开始流动？

(10分)、“拔火罐”是一种中医疗法，为了探究“火罐”的“吸力”，某人设计了如下图实验。圆柱状气缸（横截面积为S）被固定在铁架台上，轻质活塞通过细线与重物m相连，将一团燃烧的轻质酒精棉球从缸底的开关K处扔到气缸内，酒精棉球熄灭时（设此时缸内温度为t°C）密闭开关K，此时活塞下的细线刚好拉直且拉力为零，而这时活塞距缸底为L.由于气缸传热良好，重物被吸起，最后重物稳定在距地面L/10处。已知环境温度为27°C不变，mg/s与1/6大气压强相当，气缸内的气体可看做理想气体，
求t值。

封闭在气缸内一定质量的理想气体由状态A变到状态D，其体积V与热力学温度关T系如图所示，该气体的摩尔质量为M，状态A的体积为V₀，温度为T₀，O、A、D三点在同一直线上，阿伏伽德罗常数为N_A。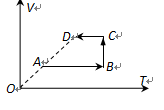

（1）由状态A变到状态D过程中     ▲      
A．气体从外界吸收热量，内能增加
B．气体体积增大，单位时间内与器壁单位面积碰撞的分子数减少
C．气体温度升高，每个气体分子的动能都会增大
D．气体的密度不变
（2）在上述过程中，气体对外做功为5J，内能增加9J，则气体    ▲  （选“吸收”或“放出”）热量  ▲  J。
（3）在状态D，该气体的密度为ρ，体积为2V₀，则状态D的温度为多少？该气体的分子数为多少？

【物理—物理3-3】
（1）下列说法中正确的是        。
a．当人们感到潮湿时，空气的绝对湿度不一定大，但相对湿度一定很大
b．在轮胎爆裂的这一短暂过程中，气体膨胀，气体温度下降
c．随着科技的发展，将来可以利用高科技手段，将散失在环境中的内能重新收集起来加以利用而不引起其他变化
d．用油膜法测出油分子的直径后，要测定阿伏加德罗常数，只需再知道油的密度即可
（2）如图所示，一直立的气缸用一质量为m的活塞封闭一定质量的理想气体，活塞横截面积为S，气体最初的体积为V₀，气体最初的压强为0.5p₀；汽缸内壁光滑且缸壁是导热的。开始活塞被固定，打开固定螺栓K，活塞下落，经过足够长时间后，活塞停在B点，设周围环境温度保持不变，已知大气压强为p₀，重力加速度为g。

①求活塞停在B点时缸内封闭气体的体积V；
②整个过程中封闭气体          （填“吸热”或“放热”），通过缸壁传递的热量Q=            。

如图，两个侧壁绝热、顶部和底部都导热的相同气缸直立放置，气缸底部和顶部均有细管连通，顶部的细管带有阀门K.两气缸的容积均为V₀气缸中各有一个绝热活塞(质量不同，厚度可忽略)。开始时K关闭，两活塞下方和右活塞上方充有气体(可视为理想气体)，压强分别为P_o和P_o/3;左活塞在气缸正中间，其上方为真空; 右活塞上方气体体积为V₀/4。现使气缸底与一恒温热源接触，平衡后左活塞升至气缸顶部，且与顶部刚好没有接触；然后打开K，经过一段时间，重新达到平衡。已知外界温度为T₀，不计活塞与气缸壁间的摩擦。求:

(i)恒温热源的温度T;
(ii)重新达到平衡后左气缸中活塞上方气体的体积V_X。

如图，一根粗细均匀的细玻璃管开口朝上竖直防止，玻璃管中有一段长为h = 24cm的水银柱封闭了一段长为x₀ = 23cm的空气柱，系统初始温度为T₀ = 200K，外界大气压恒定不变为P₀ = 76cmHg．现将玻璃管开口封闭，将系统温度升至T = 400K，结果发现管中水银柱上升了2cm，若空气可以看作理想气体，试求：

i. 升温后玻璃管内封闭的上下两部分空气的压强分别为多少cmHg？
ii. 玻璃管总长为多少？

(9分)如图所示，气缸放置在水平平台上，活塞质量为10 kg，横截面积为50 cm²，厚度为1 cm，气缸全长为21 cm，大气压强为1×10⁵ Pa，当温度为7 ℃时，活塞封闭的气柱长10 cm，若将气缸倒过来放置时，活塞下方的空气能通过平台上的缺口与大气相通．(g取10 m/s²，不计活塞与气缸之间的摩擦，计算结果保留三位有效数字)
①将气缸倒过来放置，若温度上升到27 ℃，求此时气柱的长度．
②汽缸倒过来放置后，若逐渐升高温度，发现活塞刚好接触平台，求此时气体的温度．

如图所示，在固定的气缸A和B中分别用活塞封闭一定质量的理想气体，活塞面积之比为S_A：S_B =  1：2.两活塞以穿过B的底部的刚性细杆相连，可沿水平方向无摩擦滑动.两个气缸都不漏气.初始时，A、B中气体的体积皆为V₀，温度皆为T₀=300K.A中气体压强p_A=1.5p₀，p₀是气缸外的大气压强.现对A加热，使其中气体的压强升到 ，同时保持B中气体的温度不变.求此时A中气体温度T_A .

一竖直放置、缸壁光滑且导热的柱形气缸内盛有一定量的氮气，被活塞分割成Ⅰ、Ⅱ两部分；达到平衡时，这两部分气体的体积相等，上部气体的压强为，如图（a）所示。若将气缸缓慢倒置，再次达到平衡时，上下两部分气体体积之比为，如图（b）所示。设外界温度不变。已知活塞面积为，重力加速度大小为，求活塞的质量。

如图所示，固定气缸两端活塞截面积分别为S₁和S₂，活塞间有轻杆相连，两活塞间为真空，摩擦不计。最初A内气体压强为p₀、体积为V₁、温度为T₁，B内气体体积为V₂、温度也为T₁。现将A内气体加热到T₂，B内气体温度始终保持不变，求：（1）活塞再达到平衡时移动的距离；（2）此时B中气体压强。

一根两端开口、横截面积为S=2cm²足够长的玻璃管竖直插入水银槽中并固定（插入水银槽中的部分足够深）。管中有一个质量不计的光滑活塞，活塞下封闭着长L=21cm的气柱，气体的温度T₁=280K，外界大气压取P₀=1.0×10⁵Pa（相当于75cm汞柱高的压强）。

①对气体加热，使其温度升高到T₂=320K，求此时气柱的长度；
②在活塞上施加一个竖直向上的拉力F=4N，保持气体的温度T₂不变，求平衡后气柱的长度及此时管内外水银面的高度差。

(9分)内壁光滑的导热气缸竖直浸放在盛有27 ℃温水的恒温水槽中，用不计质量的活塞封闭了压强为1.0×10⁵ Pa、体积为2.0×10^-3 m³的理想气体。现在活塞上方缓缓倒上质量为0.5 kg的沙子，封闭气体的体积变为V₁；然后将气缸移出水槽，经过缓慢降温，气体温度最终变为-23 ℃。已知活塞面积为2.0×10^-4 m²，大气压强为1.0×10⁵ Pa，g取10 m/s²，求：

(i)气体体积V₁．
(ii)气缸内气体的最终体积V₂(结果保留两位有效数字)。

一定质量的理想气体被活塞封闭在竖直放置的圆形气缸内，汽缸壁导热良好，活塞可沿汽缸壁无摩擦地滑动。开始时气体压强为，活塞下表面相对于气缸底部的高度为，外界的温度为。现取质量为的沙子缓慢地倒在活塞的上表面，沙子倒完时，活塞下降了。若此后外界的温度变为，求重新达到平衡后气体的体积。已知外界大气的压强始终保持不变，重力加速度大小为。

）如图所示，内径粗细均匀的U形管，右侧B管上端封闭，左侧A管上端开口，管内注入水银，并在A管内装配有光滑的、质量可以不计的活塞，使两管中均封入L=25cm的空气柱，活塞上方的大气压强为=76cmHg，这时两管内水银面高度差h=6cm．今用外力竖直向上缓慢地拉活塞，直至使两管中水银面相平．设温度保持不变，则：A管中活塞向上移动距离是多少？