一定质量的理想气体从状态A变化到状态B，再变化到状态C，其状态变化过程的p－V图象如图所示．已知该气体在状态A时的温度为27℃，求：
①该气体在状态B、C时的温度分别是多少？
②该气体从状态A到状态C的过程中内能的变化量是多少？
③该气体从状态A到状态C的过程中是吸热还是放热？传递的热量是多少？
如图所示，用轻质活塞在气缸内封闭一定质量理想气体，活塞与气缸壁间摩擦忽略不计，开始时活塞距气缸底高度h1 =" 0.50" m。给气缸加热，活塞缓慢上升到距离气缸底h2 =" 0.80" m处，同时缸内气体吸收Q =" 450" J的热量。已知活塞横截面积S = 5.0×10-3 m2，大气压强p0 = 1.0×105 Pa。求：
①缸内气体对活塞所做的功W；
②此过程中缸内气体增加的内能ΔU。
如图所示，用导热性能良好的气缸和活塞封闭一定质量的理想气体，气体的体积V1=8.0×10﹣3m3，温度T1=4.0×102K．现使外界环境温度缓慢降低至T2，此过程中气体放出热量7.0×102J，内能减少了5.0×102J．不计活塞的质量及活塞与气缸间的摩擦，外界大气压强p0=1.0×105Pa．求T2的值．
湖水深10m，上下水温可认为相同，在湖底形成体积为1cm3的气泡，当气泡上升到湖面时的体积是多大（大气压强取1×105Pa，湖水密度取1×103kg/m3）？气泡在上升的过程中是吸热还是放热？简要说明你判断的理由。
某学习小组做了如下实验：先把空的烧瓶放入冰箱冷冻，取出烧瓶，并迅速把一个气球紧套在烧瓶颈上，封闭了一部分气体，然后将烧瓶放进盛满热水的烧杯里，气球逐渐膨胀起来，如图。
⑴．(4分)在气球膨胀过程中，下列说法中正确的是 ；
| A．该密闭气体分子间的作用力增大 | B．该密闭气体组成的系统内能增加 |
| C．该密闭气体的压强是由于气体重力而产生的 | D．该密闭气体的体积是所有气体分子的体积之和 |
⑵．(4分)若某时刻该密闭气体的体积为V，密度为ρ，平均摩尔质量为M，阿伏加德罗常数为NA，则该密闭气体的分子个数为 ；
⑶．(4分)若将该密闭气体视为理想气体，气球逐渐膨胀起来的过程中，气体对外做了0.6J的功，同时吸收了0.9J的热量，则该气体内能变化了 J；若气球在膨胀过程中迅速脱离瓶颈，则该气球内气体的温度 (填“升高”或“降低”)。
如图所示，一直立的汽缸用一质量为m的活塞封闭一定质量的理想气体，活塞横截面积为S，气体最初的体积为V0，气体最初的压强为p0/2，汽缸内壁光滑且缸壁是导热的。开始活塞被固定，打开固定螺栓K，活塞下落，经过足够长时间后，活塞停在B点，设周围环境温度保持不变，已知大气压强为p0，重力加速度为g。若一定质量理想气体的内能仅由温度决定，求：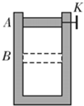
①活塞停在B点时缸内封闭气体的体积V；
②整个过程中通过缸壁传递的热量Q。
如图所示，A、B气缸的长度均为60 cm，截面积均为40 cm2，C是可在气缸内无摩擦滑动的、体积不计的活塞，D为阀门．整个装置均由导热材料制成．原来阀门关闭，A内有压强PA = 2.4×105 Pa的氧气．B内有压强PB = 1.2×105 Pa的氢气．阀门打开后，活塞C向右移动，最后达到平衡．（假定氧气和氢气均视为理想气体，连接气缸的管道体积可忽略，环境温度不变）求：
（1）活塞C移动的距离及平衡后B中气体的压强；
（2）活塞C移动过程中B中气体是吸热还是放热（简要说明理由）．
（1）下列说法正确的是 。
| A．同种物质不可能以晶体或非晶体两种形态出现 |
| B．冰融化为同温度的水时，分子势能增加 |
| C．分子间引力随距离增大而减小，而斥力随距离增大而增大 |
| D．大量分子做无规则运动的速率有大有小，所以分子速率分布没有规律 |
（2）已知二氧化碳摩尔质量为M ，阿伏加德罗常数为N A，在海面处容器内二氧化碳气体的密度为ρ。现有该状态下体积为V 的二氧化碳，则含有的分子数为 。实验表明，在2500m深海中，二氧化碳浓缩成近似固体的硬胶体。将二氧化碳分子看作直径为D的球，则该容器内二氧化碳气体全部变成硬胶体后体积约为 。
（3）如图，一定质量的理想气体从状态A 变化到状态B ，内能增加了10J。已知该气体在状态A 时的体积为1.0×l0 -3 m3。求：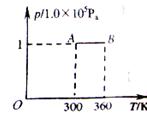
①该气体在状态B 时的体积；
②该气体从状态A 到状态B 的过程中，气体与外界传递的热量。
如图所示p－V图中，一定质量的理想气体由状态A经过 ACB过程至状态B，气体对外做功280J，放出热量410J；气体又从状态B经BDA过程回到状态A，这一过程中外界对气体做功200J。
（i）ACB过程中气体的内能如何变化？变化了多少？
（ii）BDA过程中气体吸收还是放出多少热量？
(1)(4分)我国已开展空气中PM 2.5浓度的监测工作。PM 2.5是指空气中直径小于2.5微米的悬浮颗粒物，可在显微镜下观察到，它漂浮在空中做无规则运动，很难自然沉降到地面，吸入后会进人血液对人体形成危害，矿物燃料燃烧时废弃物的排放是形成PM 2.5的主要原因。下列关于PM 2.5的说法中正确的 (填写选项前的字母)
| A．PM 2.5在空气中的运动属于分子热运动 |
| B．温度越高，PM 2.5的无规则运动越剧烈 |
| C．PM 2.5的质量越小，其无规则运动越剧烈 |
| D．由于周围大量空气分子对PM 2.5碰撞的不平衡，使其在空中做无规则运动 |
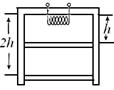
（2）(8分)如图所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体。活塞的质量为m,横截面积为S0 。初始时气体的温度为T0，活塞与容器底部相距h。现通过电热丝缓慢加热气体，当气体吸收热量Q时活塞下降了h，已知大气压强为p0，重力加速度为g,不计活塞与气缸的摩擦。求此时气体的温度和加热过程中气体内能的增加量。（题中各物理量单位均为国际单位制单位）
某学习小组做了如下实验：先把空的烧瓶放入冰箱冷冻，取出烧瓶，并迅速把一个气球紧套在烧瓶颈上，封闭了一部分气体，然后将烧瓶放进盛满热水的烧杯里，气球逐渐膨胀起来，如图。
(1)在气球膨胀过程中，下列说法正确的是
| A．该密闭气体分子间的作用力增大 |
| B．该密闭气体组成的系统熵增加 |
| C．该密闭气体的压强是由于气体重力而产生的 |
| D．该密闭气体的体积是所有气体分子的体积之和 |
(2)(4分)若某时刻该密闭气体的体积为V，密度为ρ，平均摩尔质量为M，阿伏加德罗常数为NA，则该密闭气体的分子个数为 ；
(3)(4分)若将该密闭气体视为理想气体，气球逐渐膨胀起来的过程中，气体对外做了0.6J的功，同时吸收了0.9J的热量，则该气体内能变化了 J；若气球在膨胀过程中迅速脱离瓶颈，则该气球内气体的温度 (填“升高”或“降低”)。
（1）某同学用同一注射器封闭了一定质量的理想气体在早晨和中午分别做了“验证玻意耳定律”的实验，中午气温高于早晨，他将实验结果绘成如图所示的
图象，则 
| A．图线Ⅰ是依据中午的实验数据画出的 |
| B．图线Ⅱ是依据中午的实验数据画出的 |
| C．气体在状态C与状态A相比，体积减小，内能增大 |
| D．气体若从状态B变化到状态C，内能一定增大，放出热量 |
（2）如图所示，在一个质量为M、横截面积为S的圆柱形导热气缸中，用活塞封闭了一部分空气，气体的体积为
，活塞与气缸壁间密封且光滑，一弹簧秤连接在活塞上，将整个气缸悬吊在天花板上．当外界气温升高（大气压保持为
）时，则弹簧秤的示数 （填“变大”、“变小”或“不变”），如在该过程中气体从外界吸收的热量为
，且气体的体积的变化量为
，则气体的内能增加量为 ．
（3）PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，其指标直接反映空气质量的好坏．若某城市PM2.5指标数为160μg/m3，则已达到重度污染的程度．若该种微粒的平均摩尔质量为40g/mol，试求该地区1m3空气含有该种微粒的数目．（结果保留1位有效数字）
一定质量的理想气体经历如图所示的A→B、B→C、C→A三个变化过程，设气体在状态A、B时的温度分别为TA和TB，已知TA="300" K，求：
（1）TB
（2）若气体从C→A的过程中做功为100J，同时吸热250J，则此过程中气体内能怎么改变？变化了多少？
一定质量的非理想气体(分子间的作用力不可忽略)，从外界吸收了4.2×105 J的热量，同时气体对外做了6×105 J的功，则：
(1)气体的内能是增加还是减少？其变化量的大小为多少焦耳？
(2)气体的分子势能是增加还是减少？
(3)分子平均动能如何变化？
在地球表面上横截面积为3×10－2 m2的圆筒内装0.6 kg的水,太阳光垂直照射了2 min,水温升高了1 ℃.设大气顶层的太阳能只有45%到达地面,试估算出太阳的全部辐射功率.(设太阳与地球表面之间的平均距离为1.5×1011 m)
粤公网安备 44130202000953号