高中物理自由振动和受迫振动试题

关于自由落体运动的加速度g，下列说法正确的是（    ）

A．重的物体g大

B．同一地点，轻、重物体的g值一样大

C．g值在地球上任何地方都一样大

D．g值在赤道处大于北极处

下述关于重力加速度g的说法中，正确的是（ ）

A．g的方向总是竖直向下	B．g的大小和物体的质量有关
C．g的大小和地理位置有关	D．g的大小和物体的形状有关

甲、乙两物体做自由落体运动，已知甲物体重是乙物体重的2倍，而甲距地面的高度是乙距地面高度的一半，下列说法正确的是(  )

A．甲物体的加速度是乙物体加速度的2倍

B．甲物体着地的速度是乙物体着地的速度的

C．甲物体下落的时间是乙物体下落的时间的

D．甲、乙两物体的末速度相同

如图所示，A、B两球用长1m的绳子相连，用手拿着A球时，B球距地h，释放A后不计空气阻力，两球落地时间差△t=0.2s，g取10m/s²，则h为多大？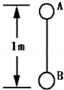

做自由落体运动的物体，在最后2秒内通过的位移是100米（ g取10m/s²），求：
⑴落到地面所需的时间
⑵物体开始下落的高度⑶落地时的速度

甲乙两球从同一高处相隔1s先后自由下落，在两球下落过程（     ）

A．两球的速度差始终保持不变	B．两球的速度差越来越大
C．两球的距离始终不变	D．两球的距离越来越大

如图所示，用小锤打击弹性金属片，A球沿水平方向抛出，同时B球自由下落，改变小球距地面的高度，多次实验均可观察到两球同时落地，这个实验现象说明A球（ ）

A．在水平方向上做匀速直线运动

B．在水平方向上做匀加速直线运动

C．在竖直方向上做匀速直线运动

D．在竖直方向上做自由落体运动

如图所示，某学习小组利用直尺估测反应时间：甲同学捏住直尺上端，使直尺保持竖直，直尺零刻度线位于乙同学的两指之间。当乙看见甲放开直尺时，立即用手指捏住直尺，根据乙手指所在位置计算反应时间。为简化计算，某同学将直尺刻度进行了改进，以相等时间间隔在直尺的反面标记反应时间的刻度线，制作了“反应时间测量仪”，下列四幅图中刻度线标度正确的是（  ）

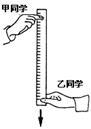
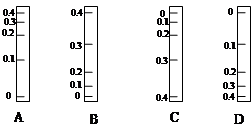
甲、乙两球从同一高度相隔1秒先后自由落下，在下落过程中

A．两球的距离始终不变	B．两球的距离越来越大
C．两球的速度差始终不变	D．两球的速度差越来越大

下列叙述中不符合历史事实的是（   ）

A．古希腊哲学家亚里士多德认为物体越重，下落得越快

B．伽利略发现亚里士多德的观点有自相矛盾的地方

C．伽利略认为，如果没有空气阻力，重物与轻物应该下落得同样快

D．伽利略用实验直接证实了自由落体运动是初速度为零的匀加速直线运动

一个小石子从离地某一高度处由静止自由落下. 某摄影爱好者恰好拍到了它下落的一段轨迹AB.该爱好者用直尺量出轨迹的长度，如图所示.已知拍摄时用的曝光时间为1/1000 s , 则小石子出发点离A点约为(     )

A.20 m   B.10 m   C.6.5 cm     D.45 m

一个从地面上竖直上抛的物体，它两次经过一个较低点A的时间间隔是，两次经过一个较高点B的时间间隔是，（不计空气阻力，）则AB之间的距离是（  ）

A．

B．

C．

D．无法确定

从离地180m的空中自由落下一个小球，取g=10m/s²，求：
（1）小球经过多少时间落到地面；
（2）小球落地时的速度；
（3）小球落地前最后1s内的位移。

伽利略对自由落体运动的研究，是科学实验和逻辑推理的完美结合．伽利略先用斜面进行实验研究，获得匀变速直线运动的规律，然后将此规律合理外推至倾角为90° ——自由落体的情形，如图所示．对伽利略研究过程的理解，下列说法正确的是（   ）

A．图中所示的情形均为真实的实验过程

B．该研究方法的核心是把实验和逻辑推理结合起来

C．利用斜面“放大”重力的作用，使实验现象更明显

D．利用斜面“冲淡”重力的作用，便于测量实验数据

如图所示，直杆长L₁=0.5m，圆筒高为L₂=2.5m。直杆位于圆筒正上方H =1m处。直杆从静止开始做自由落体运动，并能竖直穿越圆筒。试求：（取g=10m/s²，）

（1）直杆下端刚好开始进入圆筒时的瞬时速度v_1。
（2）直杆穿越圆筒所用的时间t。