如图,一质量为 、长度为 的均匀柔软细绳PQ竖直悬挂。用外力将绳的下端Q缓慢地竖直向上拉起至M点,M点与绳的上端P相距 。重力加速度大小为 。在此过程中,外力做的功为( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,abc是垂直面内的光滑固定轨道,ab水平,长度为2R:bc是半径为R的四分之一的圆弧,与ac相切于b点。一质量为m的小球。始终受到与重力大小相等的水平外力的作用,自a点从静止开始向右运动,重力加速度大小为g。小球从a点开始运动到其他轨迹最高点,机械能的增量为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,小球套在光滑的竖直杆上,轻弹簧一端固定于O点,另一端与小球相连.现将小球从M点由静止释放,它在下降的过程中经过了N点.已知M、N两点处,弹簧对小球的弹力大小相等,且 .在小球从M点运动到N点的过程中( )

A.弹力对小球先做正功后做负功
B.有两个时刻小球的加速度等于重力加速度
C.弹簧长度最短时,弹力对小球做功的功率为零
D.小球到达N点时的动能等于其在M.N两点的重力势能
在星球
上将一轻弹簧竖直固定在水平桌面上,把物体P轻放在弹簧上端,P由静止向下运动,物体的加速度a与弹簧的压缩量x间的关系如图中实线所示。在另一星球N上用完全相同的弹簧,改用物体Q完成同样的过程,其
关系如图中虚线所示,假设两星球均为质量均匀分布的球体。已知星球M的半径是星球N的3倍,则( )

A.M与N的密度相等
B.Q的质量是P的3倍
C.Q下落过程中的最大动能是P的4倍
D.Q下落过程中弹簧的最大压缩量是P的4倍
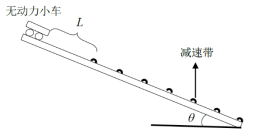
如图,一倾角为 θ的光滑斜面上有50个减速带(图中未完全画出),相邻减速带间的距离均为 d,减速带的宽度远小于 d;一质量为 m的无动力小车(可视为质点)从距第一个减速带 L处由静止释放。已知小车通过减速带损失的机械能与到达减速带时的速度有关。观察发现,小车通过第30个减速带后,在相邻减速带间的平均速度均相同。小车通过第50个减速带后立刻进入与斜面光滑连接的水平地面,继续滑行距离 s后停下。已知小车与地面间的动摩擦因数为 μ,重力加速度大小为 g。
(1)求小车通过第30个减速带后,经过每一个减速带时损失的机械能;
(2)求小车通过前30个减速带的过程中在每一个减速带上平均损失的机械能;
(3)若小车在前30个减速带上平均每一个损失的机械能大于之后每一个减速带上损失的机械能,则 L应满足什么条件?
一质量为 m的物体自倾角为 α的固定斜面底端沿斜面向上滑动。该物体开始滑动时的动能为 E k,向上滑动一段距离后速度减小为零;此后物体向下滑动,到达斜面底端时动能为 。已知sin α=0.6,重力加速度大小为g。则( )
| A. |
物体向上滑动的距离为 |
| B. |
物体向下滑动时的加速度大小为 |
| C. |
物体与斜面间的动摩擦因数等于0.5 |
| D. |
物体向上滑动所用的时间比向下滑动的时间长 |
如图所示,质量为 的物块 放置在光滑水平桌面上,右侧连接一固定于墙面的水平轻绳,左侧通过一倾斜轻绳跨过光滑定滑轮与一竖直轻弹簧相连。现将质量为 的钩码 挂于弹簧下端,当弹簧处于原长时,将 由静止释放,当 下降到最低点时(未着地), 对水平桌面的压力刚好为零。轻绳不可伸长,弹簧始终在弹性限度内,物块 始终处于静止状态。以下判断正确的是

| A. |
|
| B. |
|
| C. |
在 从释放位置运动到最低点的过程中,所受合力对 先做正功后做负功 |
| D. |
在 从释放位置运动到速度最大的过程中, 克服弹簧弹力做的功等于 机械能的减少量 |
如图,相距 的两平台位于同一水平面内,二者之间用传送带相接。传送带向右匀速运动,其速度的大小 可以由驱动系统根据需要设定。质量 的载物箱(可视为质点),以初速度 自左侧平台滑上传送带。载物箱与传送带间的动摩擦因数 ,重力加速度取 。
(1)若 ,求载物箱通过传送带所需的时间;
(2)求载物箱到达右侧平台时所能达到的最大速度和最小速度;
(3)若 ,载物箱滑上传送带△ 后,传送带速度突然变为零。求载物箱从左侧平台向右侧平台运动的过程中,传送带对它的冲量。

甲、乙两个物块在光滑水平桌面上沿同一直线运动,甲追上乙,并与乙发生碰撞,碰撞前后甲、乙的速度随时间的变化如图中实线所示。已知甲的质量为 ,则碰撞过程两物块损失的机械能为

| A. |
|
B. |
|
C. |
|
D. |
|