高中物理动能定理计算题

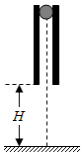
如图，一竖直圆管质量为 $M$，下端距水平地面的高度为 $H$，顶端塞有一质量为 $m$的小球。圆管由静止自由下落，与地面发生多次弹性碰撞，且每次碰撞时间均极短；在运动过程中，管始终保持竖直。已知 $M=4m$，球和管之间的滑动摩擦力大小为 $4\mathit{mg}$， $g$为重力加速度的大小，不计空气阻力。

（1）求管第一次与地面碰撞后的瞬间，管和球各自的加速度大小；

（2）管第一次落地弹起后，在上升过程中球没有从管中滑出，求管上升的最大高度；

（3）管第二次落地弹起的上升过程中，球仍没有从管中滑出，求圆管长度应满足的条件。

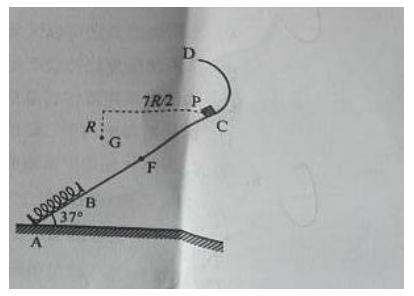
如图, 一轻弹簧原长为 $2R$, 其一端固定在倾角为 ${37}^{\circ }$ 的固定直轨道 $\mathit{AC}$ 的底端 $A$处, 另一端位于直轨道上 $\mathrm{B}$ 处, 弹簧处于自然状态, 直轨道与一半径为 $\frac{5}{6}R$ 的光滑圆弧轨道相切于 $C$ 点, $\mathit{AC}=7R,A,B\mathrm{、}C,D$ 均在同一竖直面内。质量为 $m$ 的小物块 $P$ 自 $C$ 点由静止开 始下滑, 最低到达 $\mathrm{E}$ 点（末画出 $)$, 随后 $\mathrm{P}$ 沿轨道被弹回, 最高点到达 $\mathrm{F}$ 点, $\mathrm{AF}=4R$, 已知 $\mathrm{P}$

与直轨道间的动摩擦因数 $\mu =\frac{1}{4}$, 重力加速度大小为 $g\mathrm{。}$ （取 $\sin {37}^{\circ }=\frac{3}{5},\cos {37}^{\circ }=\frac{4}{5}$ )

(1) 求 P 第一次运动到 $\mathrm{B}$ 点时速度的大小。

(2) 求 $\mathrm{P}$ 运动到 $\mathrm{E}$ 点时弹簧的弹性势能。

(3) 改变物块 $\mathrm{P}$ 的质量, 将 $\mathrm{P}$ 推至 $\mathrm{E}$ 点, 从静止开始释放。已知 $\mathrm{P}$ 自圆弧轨道的最高点 $\mathrm{D}$ 处水平飞出后, 恰好通过 $G$ 点。 $G$ 点在 $C$ 点左下方，与 $C$ 点水平相距 $\frac{7}{2}R$ 、竖直相距 $R$, 求 $\mathrm{P}$ 运动到 D 点时速度的大小和改变后 P 的质量。

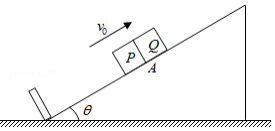
如图所示，一倾角为 $\theta$的固定斜面的底端安装一弹性挡板， $P$、 $Q$两物块的质量分别为 $m$和 $4m$， $Q$静止于斜面上 $A$处。某时刻， $P$以沿斜面向上的速度 $v_0$与 $Q$发生弹性碰撞。 $Q$与斜面间的动摩擦因数等于 $\tan \theta$，设最大静摩擦力等于滑动摩擦力。 $P$与斜面间无摩擦，与挡板之间的碰撞无动能损失。两物块均可以看作质点，斜面足够长， $Q$的速度减为零之前 $P$不会与之发生碰撞。重力加速度大小为 $g$。

（1）求 $P$与 $Q$第一次碰撞后瞬间各自的速度大小 $v_{P1}$、 $v_{Q1}$；

（2）求第 $n$次碰撞使物块 $Q$上升的高度 $h_n$；

（3）求物块 $Q$从 $A$点上升的总高度 $H$；

（4）为保证在 $Q$的速度减为零之前 $P$不会与之发生碰撞，求 $A$点与挡板之间的最小距离 $s$。