某同步卫星距地面高度为h,已知地球半径为R,表面的重力加速度为g,地球自转的角速度为ω,则该卫星的周期为
A. |
B. |
C. |
D. |
发射地球同步卫星要经过三个阶段:先将卫星发射至近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3。轨道1、2相切于Q点,轨道2、3相切于P点,如图所示。当卫星分别在1、2、3轨道上正常运行时,其中说法正确的是( )
| A.卫星在轨道1上经过Q点时的加速度等于它在轨道2 上经过 Q点时的加速度 |
| B.卫星在轨道3上的动能小于它在轨道1上的动能 |
| C.卫星在轨道3上的引力势能小于它在轨道1上的引力势能 |
| D.卫星在轨道3上的机械能大于它在轨道1上的机械能 |
2012年6月16日,“神舟九号”宇宙飞船搭载3名航天员飞天,并于6月18日14∶00与“天宫一号”成功对接。在发射时,“神舟九号”宇宙飞船首先要发射到离地面很近的圆轨道,然后经过多次变轨后,最终与在距地面高度为h的圆形轨道上绕地球飞行的“天宫一号”完成对接,之后,整体保持在距地面高度仍为h的圆形轨道上绕地球继续运行.已知地球半径为R,地面附近的重力加速度为g。求:
(1)地球的第一宇宙速度;
(2)“神舟九号”宇宙飞船在近地圆轨道运行的速度与对接后整体的运行速度之比。
如图所示,一航天器围绕地球沿椭圆形轨道运动,地球的球心位于该椭圆的一个焦点上,A.B两点分别是航天器运行轨道上的近地点和远地点,若航天器所受阻力可以忽略不计,则该航天器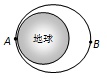
A.由近地点A运动到远地点B的过程中动能增大
B.由近地点A运动到远地点B的过程中万有引力做正功
C.在近地点A的加速度小于它在远地点B的加速度
D.运动到A点时其速度如果能增加到第二宇宙速度,那么它将不再围绕地球运行
如图为“高分一号”卫星与北斗导航系统中的“G1”卫星,在空中某一平面内绕地心O做匀速圆周运动的示意图。已知卫星“G1”的轨道半径为r,地球表面的重力加速度为g,地球半径为R,万有引力常量为G。则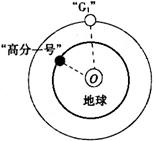
| A.“高分一号”的加速度小于卫星“G1”的加速度 |
| B.“高分一号”的运行速度大于第一宇宙速度 |
C.地球的质量为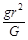 |
D.卫星“G1”的周期为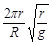 |
某一火星探测器环绕火星做“近地”匀速圆周运动,测得该探测器运动的周期为T,则火星的平均密度ρ的表达式为(k是一个常数)( )
A.ρ= |
B.ρ=kT | C.ρ= |
D.ρ=kT2 |
【改编】飞船B与空间站A交会对接前绕地球做匀速圆周运动的位置如图所示,虚线为各自的轨道,则( )

A.A的周期小于B的周期
B.A的加速度大于B的加速度
C.要使B追上A实现对接,需使B加速
D.A、B的发射速度小于第一宇宙速度
我国航天事业取得了突飞猛进地发展,航天技术位于世界前列,在航天控制中心对其正上方某卫星测控时,测得从发送“操作指令”到接收到卫星“已操作”的信息需要的时间为2t(设卫星接收到“操作指令”后立即操作,并立即发送“已操作”的信息到控制中心),测得该卫星运行周期为T,地球半径为R,电磁波的传播速度为c,由此可以求出地球的质量为( )
A. |
B. |
C. |
D.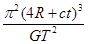 |
设人造地球卫星绕地球做匀速圆周运动,卫星离地面越高,则卫星的( )
| A.速度越大 | B.角速度越大 |
| C.向心加速度越大; | D.周期越长 |
我国自主研制的北斗卫星导航系统包括5颗静止轨道卫星(同步卫星)和30颗非静止轨道卫星,将为全球用户提供高精度、高可靠性的定位、导航服务。
A为地球同步卫星,质量为m1;B为绕地球做圆周运动的非静止轨道卫星,质量为m2,离地面高度为h.已知地球半径为R,地球自转周期为T0,地球表面的重力加速度为g。 求:
(1)卫星A运行的角速度;(2)卫星B运行的线速度。
研究表明,地球自转在逐渐改变,3亿年前地球自转的周期约为22小时。假设这种趋势会持续下去,且地球的质量、半径都不变,若干年后( )
| A.近地卫星(以地球半径为轨道半径)的运行速度比现在大 |
| B.近地卫星(以地球半径为轨道半径)的向心加速度比现在小 |
| C.同步卫星的运行速度比现在小 |
| D.同步卫星的向心加速度与现在相同 |
地球同步卫星轨道必须在赤道平面上空和地球有相同的角速度,才能和地球保持相对静止.关于各国发射的地球同步卫星,下列表述正确的是( ).
| A.所受的万有引力大小一定相等 |
| B.离地面的高度一定相同 |
| C.运行的速度都小于7.9 km/s |
| D.都位于赤道上空的同一个点 |
2013年6月,我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接.如图所示,已知“神舟十号”从捕获“天宫一号”到实现对接用时t,这段时间内组合体绕地球转过的角度为θ(此过程轨道不变,速度大小不变),地球半径为R,地球表面重力加速度为g,万有引力恒量G,不考虑地球自转;求:(1)地球质量M;(2)组合体运动的周期T;(3)组合体所在圆轨道离地高度H。
如图所示,飞行器P绕某星球做匀速圆周运动,星球相对飞行器的张角为θ,下列说法正确的是( )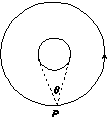
| A.轨道半径越大,周期越长 |
| B.轨道半径越大,速度越大 |
| C.若测得周期和张角,可得到星球的平均密度 |
| D.若测得周期和轨道半径,可得到星球的平均密度 |