2007 年3 月26 日,中俄共同签署了《中国国家航天局和俄罗斯联邦航天局关于联合探测火星——火卫一合作的协议》,双方确定2008年联合对火星及其卫星“火卫一”进行探测.“火卫一”在火星赤道正上方运行,与火星中心的距离为9450km.绕火星1周需7h39min,若其绕行轨道简化为圆轨道,引力常量G已知.则由以上信息能求出
| A.火星的质量 | B.火星的密度 |
| C.“火卫一”的质量 | D.“火卫一”受到火星的引力 |
2001年7月哈勃空间望远镜拍摄了如图所示被称为哈氏天体的环状星系,星系外面是主要由明亮蓝星组成的环,而中心附近是较红的年老恒星,就像我们的银河系一样,这个环曾经也是一个标准的巨大星系,然而有一天,一个更小的星系却从一侧猛击这个星系,并贯穿了恒星系盘,入侵者的引力最初将星系内星体与气体牵引至受害者的中心,随后,当较小的星系穿过大星系的恒星盘,并从另一侧出现后,星体与气体又向外反弹,从而形成了一个扩大的环,你认为下列说法合理的是( )

| A.若知道受撞击前该星系最外侧轨道恒星绕中心运动周期、半径,可估算星系总质量 |
| B.小星系从星盘中央穿过时,引力增大使得巨大星系内星体离开原轨道做靠近中心的运动 |
| C.小星系从星盘中央穿过后,引力减小使得巨大星系内星体做离心运动 |
| D.星系环内所有星体绕中心旋转半径三次方与周期平方比值一定相等 |
我国月球探测计划“嫦娥工程”已经启动,科学家对月球的探索会越来越深入。
(1)若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,月球绕地球的运动近似看做匀速圆周运动,试求出月球绕地球运动的轨道半径;
(2)若宇航员随登月飞船登陆月球后,在月球表面高度为h的某处以速度v0水平抛出一个小球,小球飞出的水平距离为x。已知月球半径为R月,引力常量为G,试求出月球的质量M月。
宇宙飞船以周期T绕地球做圆周运动时,由于地球遮挡阳光,会经历“日全食”过程,如图所示.已知地球的半径为R,地球质量为M,引力常量为G,地球自转周期为T0太阳光可看做平行光,宇航员在A点测出的张角为 ,则以下判断不正确的是
,则以下判断不正确的是
A.飞船绕地球运动的线速度为 |
B.一天内飞船经历“日全食”的次数为 |
C.飞船每次“日全食”过程的时间为 |
D.飞船周期为 |
2013年我国相继完成“神十”与“天宫”对接、“嫦娥”携“玉兔”落月两大航天工程。某航天爱好者提出“玉兔”回家的设想:如图,将携带“玉兔”的返回系统由月球表面发射到h高度的轨道上,与在该轨道绕月球做圆周运动的飞船对接,然后由飞船送“玉兔”返回地球。设“玉兔”质量为m,月球为R,月面的重力加速度为g月。以月面为零势能面。“玉兔”在h高度的引力势能可表示为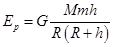 ,其中G为引力常量,M为月球质量,若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
,其中G为引力常量,M为月球质量,若忽略月球的自转,从开始发射到对接完成需要对“玉兔”做的功为( )
A.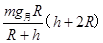 |
B.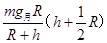 |
C.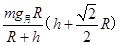 |
D.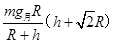 |
有一颗与地球同步静止轨道卫星在同一轨道平面的人造地球卫星,自西向东绕地球运行。已知它的运行半径为同步轨道半径的四分之一,地球自转周期为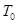 ,则该卫星需要相隔多长时间才在赤道上同一城市的正上方再次出现( )
,则该卫星需要相隔多长时间才在赤道上同一城市的正上方再次出现( )
A.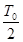 |
B.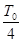 |
C.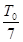 |
D.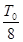 |
我国发射了一颗地球资源探测卫星,发射时,先将卫星发射至距离地面50km的近地圆轨 道1 上:,然后变轨到近地点距离地面50km、远地点距离地面1500km的椭圆轨道2上,最后由轨道2进入半径为7900km的圆轨道3,轨道1、2相切于P点,轨道2、3相切于Q点。忽略空气阻力和卫星质量的变化,则以下说法正确的是
| A.该卫星从轨道1变轨到轨道2需要在P处点火加速 |
| B.该卫星在轨道2上稳定运行时,P点的速度小于Q点的速度 |
| C.该卫星在轨道2上Q点的加速度大于在轨道3上Q点的加速度 |
| D.该卫星在轨道3的机械能小于在轨道1的机械能 |
两颗卫星在同一轨道平面绕地球做匀速圆周运动,地球半径为R,a卫星离地面的高度等于R,a卫星离地面高度为3R,则
(1)a、b两卫星周期之比Ta∶Tb是多少?
(2)若某时刻两卫星正好同时通过地面同一点的正上方,则a至少经过多少个周期两卫星相距最远?
发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送人同步圆轨道3,轨道1、2相切于Q点,轨道2、3相切于P点.如图所示,则卫星分别在1、2、3轨道上运行时,以下说法正确的是( )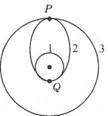
| A.卫星在轨道3上的速率大于在轨道1上的速率 |
| B.卫星在轨道3上的角速度小于在轨道1上的角速度 |
| C.卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 |
| D.卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度 |
有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则
| A.a的向心加速度等于重力加速度g |
| B.在相同时间内b转过的弧长最长 |
C.c在4 h内转过的圆心角是 |
| D.d的运动周期有可能是20 h |
已知地球的半径为6.4×106m,地球自转的角速度为7.27×10-5rad/s,地球表面的重力加速度为9.8 m/s2,在地球表面发射卫星的第一宇宙速度为7.9×103m/s,第三宇宙速度为16.7×103m/s,月地中心间距离为3.84×108m.假设地球上有一棵苹果树长到月球那么高,则当苹果脱离苹果树后,请计算此时苹果线速度判断,苹果将不会( )
| A.落回地面 | B.成为地球的“苹果月亮” |
| C.成为地球的同步“苹果卫星” | D.飞向茫茫宇宙 |
地球赤道上有一物体随地球的自转而做圆周运动,所受的向心力为F1,向心加速度为a1,线速度为v1,角速度为ω1;绕地球表面附近做圆周运动的人造卫星(高度忽略)所受的向心力为F2,向心加速度为a2,线速度为v2,角速度为ω2;地球同步卫星所受的向心力为F3,向心加速度为a3,线速度为v3,角速度为ω3;地球表面重力加速度为g,第一宇宙速度为v,假设三者质量相等,则( )
A. |
B. |
C.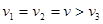 |
D. |
人造卫星A,B绕地球做匀速圆周运动,A卫星的运行周期为2天,A轨道半径为B轨道半径的1/3,则B卫星运行的周期大约是( )
| A.1~4天 | B.4~8天 |
| C.8~16天 | D.16~20天 |
如图所示,有A、B两颗卫星绕地心O做圆周运动,旋转方向相同.A卫星的周期为T1,B卫星的周期为T2,在某一时刻两卫星相距最近,则(引力常量为G)
A.两卫星经过时间t= T1+ T2再次相距最近
B.两颗卫星的轨道半径之比T22:T12
C.若己知两颗卫星相距最近时的距离,可求出地球的质量
D.若己知两颗卫星相距最近时的距离,可求出地球表面的重力加速度