下列几组数据中能算出地球质量的是（万有引力常量G是已知的）
| A．地球绕太阳运行的周期T和地球中心离太阳中心的距离r |
| B．月球绕地球运行的周期T和地球的半径r |
| C．月球绕地球运动的角速度和月球中心离地球中心的距离r |
| D．月球绕地球运动的周期T和轨道半径r |
科学家们推测，太阳系的第十颗行星就在地球的轨道上，从地球上看，它永远在太阳的背面，人类一直未能发现它，可以说是“隐居”着的地球的“孪生兄弟”．由以上信息可以确定：（ ）
| A．这颗行星的公转周期与地球相等 |
| B．这颗行星的半径等于地球的半径 |
| C．这颗行星的密度等于地球的密度 |
| D．这颗行星上同样存在着生命 |
1990年4月25日，科学家将哈勃天文望远镜送上距地球表面约600km的高空．使得人类对宇宙中星体的观测与研究有了极大的进展．假设哈勃天文望远镜沿圆轨道绕地球运行．已知地球半径为6．4×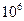
m，利用地球同步卫星与地球表面的距离为3.6×
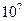m这一事实可得到哈勃天文望远镜绕地球运行的周期．以下数据中最接近其运行周期的是 ( )
A．0.6小时 |
B．1.6小时 |
C．4.0小时 | D．24小时 |
已知万有引力常量G，那么在下列给出的各种情景中，能根据测量的数据求出火星平均密度的是
| A．在火星表面使一个小球做自由落体运动，测出下落的高度H和时间t |
| B．发射一颗贴近火星表面绕火星做圆周运动的飞船，测出飞船的周期T |
| C．观察火星绕太阳的圆周运动，测出火星的直径D和火星绕太阳运行的周期T |
| D．发射一颗绕火星做圆周运动的卫星，测出卫星绕火星运行的轨道半径r和卫星的周期T |
设想地球没有自转，竖直向下通过地心把地球钻通。如果在这个通过地心的笔直的管道的一端无初速度地放下一物体，下列说法正确的是（ ）
| A．物体在地心时，它与地心间距离为零，地球对物体的万有引力无穷大 |
| B．物体在地心时，地球对它的万有引力为零 |
| C．物体在管道中将往返运动，通过地心时加速度为零，速率最大 |
| D．物体运动到地心时由于万有引力为零，它将静止在地心不动 |
关于万有引力定律，下列说法不正确的是：
| A．牛顿借助自己的力学成就对前人的研究成果进行分析，总结出万有引力定律 |
| B．卡文迪许用扭秤实验证明万有引力定律是正确的，并测出万有引力恒量 |
| C．万有引力恒量的单位可以用Ｎ·kg2／m2 |
| D．万有引力定律仅适用于天体之间 |
木星是绕太阳运行的行星之一，而木星的周围又有卫星绕其运行。如果要通过观测求得木星的质量，则需要测量的量是 （ ）
| A．木星运行的周期和轨道半径 | B．卫星运行的周期和轨道半径 |
| C．木星运行的周期和卫星的轨道半径 | D．卫星运行的周期和木星的轨道半径 |
已知地球质量为M，半径为R，设想把一质量为m的物体置于地心。则该物体与地球间的万有引力大小是：
| A．零 | B．无穷大 | C．GMm/R2 | D．无法确定 |
在讨论地球潮汐成因时，地球绕太阳运行轨道与月球绕地球运行轨道可视为圆轨道．已知太阳质量约为月球质量的2.7×107倍，地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的400倍．关于太阳和月球对地球上相同质量海水的引力，以下说法正确的是
| A．太阳引力远大于月球引力 |
| B．太阳引力与月球引力相差不大 |
| C．月球对不同区域海水的吸引力大小相等 |
| D．月球对不同区域海水的吸引力大小有差异 |
两个物体之间的万有引力大小为
，若两物之间的距离减小x，两物体仍可视为质点，此时两个物体之间的万有引力大小为
，根据上述条件可以计算（ ）
| A．两物体的质量 |
| B．万有引力常数 |
| C．两物体之间的距离 |
| D．条件不足，无法计算上述选项中的任何一个物理量 |
某物体在地面上受到地球对它的万有引力为F．若此物体受到的引力减小到
，则此物体距离地面的高度应为（R为地球半径）
| A．R | B．2R | C．4R | D．8R |
人造卫星离地面距离等于地球半径R，卫星以速度v沿圆轨道运动，设地面的重力加速度为g，则有：（ ）
A．v = |
B．v = |
C．v = |
D．v= |
牛顿发现的万有引力定律是科学史上最伟大的定律之一，在天体运动中起着决定性作用。万有引力定律告诉我们，两物体间的万有引力（ ）
| A．与它们间的距离成正比 | B．与它们间的距离成反比 |
| C．与它们间距离的二次方成正比 | D．与它们间距离的二次方成反比 |
，重力加速度
，地球半径
，则可知地球质量的数量级是（ ）
粤公网安备 44130202000953号