高中物理万有引力定律及其应用试题

已知某行星半径为R，以某第一宇宙速度运行的卫星的绕行周期为T，围绕该行星运动的同步卫星运行速率为v，则该行星的自转周期为：

A．

B．

C．

D．

设地球是一质量分布均匀的球体，O为地心．已知质量分布均匀的球壳对壳内物体的引力为零．在下列四个图中，能正确描述x轴上各点的重力加速度g的分布情况的是(　　)．

2003年10月15日，我国神舟五号载人飞船成功发射.标志着我国的航天事业发展到了一个很高的水平.飞船在绕地球飞行的第5圈进行变轨，由原来的椭圆轨道变为距地面高度为R的圆形轨道.已知地球半径为R，地面处的重力加速度为g，引力常量为G,求：
⑴地球的质量；
⑵飞船在上述圆形轨道上运行的周期T.

某研究性学习小组首先根据小孔成像原理估测太阳半径，再利用万有引力定律估算太阳的密度.准备的器材有:①不透光圆筒，一端封上不透光的厚纸，其中心扎一小孔，另一端封上透光的薄纸；②毫米刻度尺.已知地球绕太阳公转的周期为T，万有引力常量为G.要求:(1)简述根据小孔成像原理估测太阳半径R的过程.(2)利用万有引力定律推算太阳密度.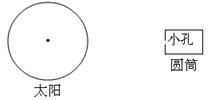

“嫦娥二号”是我国月球探测第二期工程的先导星．若测得“嫦娥二号”在月球(可视为密度均匀的球体)表面附近圆形轨道运行的周期为T，已知引力常量为G，半径为R的球体体积公式V＝πR³，则可估算月球的(  )．

A．半径

B．质量

C．密度

D．自转周期

据报道，北京时间2012年5月5日夜晚，天空中出现“超级月亮”，这是2012年的最大满月．实际上，月球绕地球运动的轨道是一个椭圆，地球在椭圆的一个焦点上．根据天文学家观测，此时月球距离地球最近，约35.7万公里，与平均距离的比值约为37∶40.有传言称由于月亮对地球的引力增大，“超级月亮”会引发严重的地震、火山或者其他自然灾害．由以上信息和学过的知识，以下说法中正确的有(　　)

A．“超级月亮”对地球上的物体引力要比平均距离时大15%左右

B．此时月球达到最大速度

C．如果要使月球以此时到地球的距离开始绕地球做圆周运动，需要使月球适当减速

D．如果已知万有引力常量G，结合以上信息，可以计算出月球的质量

同步卫星是在地球的赤道上空圆形轨道围绕地球转，和地球同步，相对地面静止，若地球表面的重力加速度为g，地球半径为R，地球自转的周期为T，求：
(1)同步卫星的圆轨道离地面的高度;
(2)同步卫星在圆轨道上运行的速率。

在火箭发射卫星的开始阶段，火箭与卫星竖直上升的运动可视为匀加速直线运动，加速度大小为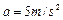，封闭舱内，弹簧测力计上挂着一个质量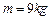的物体，在卫星上升到某高度时，弹簧测力计示数为85N，求此时卫星与地面间的距离(地球半径为)

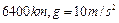2007年10月24日，“嫦娥一号”成功发射，11月5日进入38万公里以外的环月轨道，11月24日传回首张图片，这是我国航天事业的又一成功。“嫦娥一号”围绕月球的运动可以看作匀速圆周运动，万有引力常量已知，如果在这次探测工程中要测量月球的质量，则需要知道的物理量有（  ）

A．“嫦娥一号”的质量和月球的半径

B．“嫦娥一号”绕月球运动的周期和轨道半径

C．月球的半径和“嫦娥一号”绕月球运动的周期

D．“嫦娥一号”的质量、月球的半径和“嫦娥一号”绕月球运动的周期

据报道，美国和俄罗斯的两颗卫星在太空相撞，相撞地点位于西伯利亚上空500英里(约805公里)．相撞卫星的碎片形成太空垃圾，并在卫星轨道附近绕地球运转，国际空间站的轨道在相撞事故地点下方270英里(434公里)．若把两颗卫星和国际空间站的轨道都看做圆形轨道，以下关于上述报道的说法正确的是

A．这两颗相撞卫星在同一轨道上

B．这两颗相撞卫星的周期、向心加速度大小一定相等

C．两相撞卫星的运行速度均大于国际空间站的速度

D．两相撞卫星的运行周期均大于国际空间站的运行周期

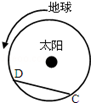
如图所示设地球的质量为M且绕太阳做匀速圆周运动，当地球运动到D点时，有一质量为m的飞船由静止开始从D点只在恒力F的作用下沿DC方向做匀加速直线运动，再过两个月，飞船在C处再次掠过地球上空，假设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向，飞船到地球表面的距离远小于地球与太阳间的距离，则地球与太阳间的万有引力大小（ ）

A．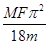

B．

C．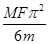

D．

如图，A为太阳系中的天王星，它绕太阳O运行的轨道视为圆时，运动的轨道半径为R₀，周期为T_o人匀速圆周运动。天文学家长期观测发现，天主星实际运动的轨道与圆轨道总有一些偏离，且每隔t_o时间发生一次最大偏离，形成这种现象的原因可能是夭王星外侧还存在着一颗未知的行星B，假设行星B与A在同一平面内，且与A的绕行方向相同，它对天王星的万有引力引起天王星轨道的偏离，由此可推测未知行星的运动轨道半径是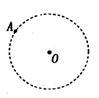

A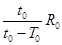．	B．
C．	D．

“嫦娥一号”卫星开始绕地球在椭圆轨道运动，经过变轨、制动后，成为一颗绕月球做圆周运动的卫星。设卫星距月球表面的高度为h ，做匀速圆周运动的周期为T 。已知月球半径为R ，引力常量为G。求：
（1）月球的质量M及月球表面的重力加速度g；
（2）在距月球表面高度为h₀的地方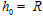（），将一质量为m的小球以v₀的初速度水平抛出，求落地瞬间月球引力对小球做功的瞬时功率P。

未来“嫦娥五号”落月后，轨道飞行器将作为中继卫星在绕月轨道上做圆周运动，如图所示．设卫星距离月球表面高为h，绕行周期为T，已知月球绕地球公转的周期为T₀，地球半径为R，地球表面的重力加速度为g，月球半径为r，万有引力常量为G．试分别求出：

（1）地球的质量和月球的质量；
（2）中继卫星向地球发送的信号到达地球，最少需要多长时间？（已知光速为c，且h≤r≤R）

理论研究表明第二宇宙速度是第一宇宙速度的倍。火星探测器悬停在距火星表面高度为h处时关闭发动机，做自由落体运动，经时间t落到火星表面。已知引力常量为G，火星的半径为R。若不考虑火星自转的影响，要使探测器脱离火星飞回地球，则探测器从火星表面的起飞速度至少为

A．

B．

C．11.2km/s

D．7.9km/s