高中物理万有引力定律及其应用试题

已知万有引力常量为G，地球半径为R，同步卫星距地面的高度为h，地球的自转周期为T，地球表面的重力加速度为g。某同学根据以上条件，提出一种估算地球赤道表面的物体随地球自转的线速度大小的方法：
地球赤道表面的物体随地球作圆周运动，由牛顿运动定律有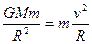
又因为地球上的物体的重力约等于万有引力，有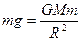
由以上两式得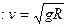
（1）请判断上面的结果是否正确？
（2）由题目给出的条件还可以估算出哪些物理量？

地球质量为M，半径为R，万有引力恒量为G。若已知第一宇宙速度=7．9k／s，地球半径R=6．4×10³km，万有引力恒量G=6．67×10N·m²·kg。
求：（1）第一宇宙速度的计算式；
（2）地球的质量（要求保留两位有效数字）。

两个星球组成双星，它们在相互之间的万有引力作用下，绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R，其运动周期为T，求两星的总质量。

中子星是恒星演化过程的一种可能结果，它的密度很大。现有一中子星，观测到它的自转周期为T=s。问该中子星的最小密度应是多少才能维持该星的稳定，不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.6710m/kg·s)

宇航员在一星球表面上的某高处，沿水平方向抛出一小球。经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L。若抛出时初速度增大到2倍，则抛出点与落地点之间的距离为L。已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G。求该星球的质量M。

设地球表面的重力加速度为g，物体在距地心4R（R是地球半径）处，由于地球的引力作用而产生的重力加速度g，，则g/g，为（）

A．1；

B．1/9；

C．1/4；

D．1/16。

如图所示，在距一质量为M、半径为R、密度均匀的球体中心2R处，有一质量为m的质点，M对m的万有引力的大小为F。现从M中挖出一半径为r的球体，如图，OO′=R/2。求M中剩下的部分对m的万有引力的大小。

在天文学中，把两颗相距较近的恒星叫双星，已知两恒星的质量分别为m和M，两星之间的距离为L，两恒星分别围绕共同的圆心作匀速圆周运动，如图所示，求恒星运动的半径和周期。

如果某行星有一颗卫星沿非常靠近此恒星的表面做匀速圆周运动的周期为T，则可估算此恒星的密度为多少?

已知地球绕太阳公转的轨道半径r=1.491011m， 公转的周期T=3.16107s，求太阳的质量M。

设想人类开发月球，不断地把月球上的矿藏搬运到地球上．假如经过长时间开采后，地球仍可看成均匀球体，月球仍沿开采前的圆轨道运动则与开采前比较

A．地球与月球间的万有引力将变大

B．地球与月球间的万有引力将减小

C．月球绕地球运动的周期将变长

D．月球绕地球运动的周期将变短