高中物理匀速圆周运动选择题

火车转弯可以看做是做匀速圆周运动，火车速度提高易使外轨受损．为解决火车高速转弯时使外轨受损这一难题，理论上可行的措施是

A．适当增大弯道半径

B．适当减小弯道半径

C．适当减小外轨道和内轨道的高度差

D．适当增加外轨道和内轨道的高度差

杂技表演“飞车走壁”的演员骑着摩托车，飞驶在光滑的圆锥形筒壁上，筒的轴线垂直于水平面，圆锥筒固定不动，演员和摩托车的总质量为m，先后在A、B两处紧贴着内壁分别在图虚线所示的水平面内做匀速圆周运动 ，下列说法不正确的是  （    ）

A.A处的线速度大于B处的线速度
B.A处的角速度小于B处的角速度
C.A处对筒的压力大于B处对筒的压力
D.A处的向心力等于B处的向心力

三个人造卫星A.B.C在地球的大气层外沿如图所示的方向做匀速圆周运动，已知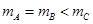，则关于三个卫星的说法中错误的是

A.线速度大小的关系是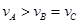
B.周期关系是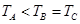
C.向心力大小的关系是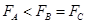
D.轨道半径和周期的关系是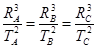

如图所示，一个内壁光滑的圆锥形筒的轴线垂直于水平面，圆锥筒固定，有质量相等的小球A和B沿着筒的内壁在水平面内作匀速圆周运动，A的运动半径较大，则下列说法正确的是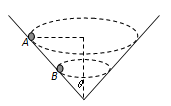

A．球A的线速度小于球B的线速度

B．球A的角速度大于球B的角速度

C．球A的加速度等于球B的加速度

D．球A对筒壁的压力大小大于球B对筒壁的压力大小

“超级地球”是指围绕恒星公转的类地行星 科学家们发现有两颗未知质量的不同“超级地球”环绕同一颗恒星公转，周期分别为10天和20天 根据上述信息可以计算两颗“超级地球”（ ）
A 质量之比
B 所受的引力之比
C 角速度之比
D 向心加速度之比

假设航天飞机在太空绕地球作匀速圆周运动．宇航员利用机械手将卫星举到机舱外，并相对航天飞机静止释放该卫星，则被释放的卫星将(不计空气阻力)（ ）

A．停留在轨道的被释放处

B．随航天飞机同步绕地球作匀速圆周运动

C．向着地球做自由落体运动

D．沿圆周轨道的切线方向做直线运动

质量为m的飞机，以速率v在水平面上做半径为r的匀速圆周运动，空气对飞机的作用力的大小等于（  ）

A．

B．

C．

D．

如图所示，半径分别为r和R的两根圆柱靠摩擦传动，已知R=2r，A、B分别在大、小圆柱的边缘上，O₂C=r，若两圆柱之间没有出现打滑现象，则A、B、C三点的角速度的比值分别为（ ）

A．2：1：2    B．2：2：1    C．1：1：2    D．1：2：1

如图甲所示，一轻杆一端固定在O点，另一端固定一小球，在竖直平面内做半径为R的圆周运动．小球运动到最高点时，杆与小球间弹力大小为F_N，小球在最高点的速度大小为v，F_N－v²图象如图乙所示．下列说法正确的是

A．当地的重力加速度大小为

B．小球的质量为

C．当v^2＝c时，杆对小球弹力方向向上

D．若v^2＝2b，则杆对小球弹力大小为2a

下列关于离心现象的说法正确的是：

A．当物体所受的离心力大于向心力时产生离心现象

B．做匀速圆周运动的物体，当它所受的一切力都突然消失时，它将做背离圆心的圆周运动

C．做匀速圆周运动的物体，当它所受的一切力都突然消失时它将沿切线做直线运动

D．做匀速圆周运动的物体，当它所受的一切力都突然消失时它将做曲线运动

下列关于运动和力的叙述中，正确的是

A．做曲线运动的物体，其加速度方向一定是变化的

B．做圆周运动的物体，所受的合力一定指向圆心

C．物体所受合力方向与运动方向相反，该物体一定做直线运动

D．物体运动的速率在增加，所受合力方向一定与运动方向相同

如图所示，甲、乙两快艇在湖面上做匀速圆周运动。关于两快艇的运动，下列说法正确的是（   ）

A．若两快艇运动的周期相等，半径较小的向心加速度较大

B．若两快艇运动的线速度大小相等，半径较小的向心加速度较大

C．若两快艇运动的角速度相等，半径较小的向心加速度较大

D．若两快艇运动的线速度大小相等，半径较大的向心加速度较大

如图所示为赛车场的一个水平“U”形弯道，转弯处为圆心在O点的半圆，内外半径分别为r和2r。一辆质量为m的赛车通过AB线经弯道到达线，有如图所示的①②③三条路线，其中路线③是以为圆心的半圆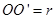，。赛车沿圆弧路线行驶时，路面对轮胎的最大径向静摩擦力均为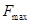。选择路线，赛车以不打滑的最大速率通过弯道（所选路线内赛车速率不变，发动机功率足够大），则：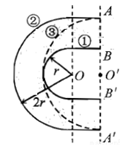

A．赛车经过路线②③时的位移相等

B．选择路线②，赛车的速率最小

C．选择路线③，赛车所用时间最短

D．①②③三条路线的圆弧上，赛车的向心加速度大小相等

如图所示为自行车的传动装置，大齿盘通过链条带动小齿盘转动时，大齿盘边缘的线速度v₁和小齿盘边缘的线速度v₂的大小关系是（ ）

A．v1＞v2

B．v1=v2

C．v1＜v2

D．不能确定

如图所示，在某外高内低的弯道测试路段上汽车向左转弯，把汽车的运动看作是在水平面内做半径为R的匀速圆周运动。设路面内外高度相差h，路基的水平宽度为d，路面的宽度为L，已知重力加速度为。要使车轮与路面之间垂直前进方向的横向摩擦力等于零，则汽车转弯时的车速应等于

A     B       C     D