在距半径为R的圆形跑道之圆心(O)L的地方有一高为h的平台,如图所示,一辆小车以速率υ在跑道上运动,从平台上以大小为υ0的水平速度向跑道抛出一小沙袋(沙袋所受空气阻力不计)
(1)当υ0取值在何范围内,小沙袋才有落入小车的可能?
(2)小车在跑道上沿逆时针方向运动,当小车经过跑道上A点时,将小沙袋以某一速率υ0瞄准跑道上的B点水平抛出(∠AOB= 90°),为确保沙袋能在B处落入小车,则小车的速率υ应满足什么条件?
高台滑雪运动员经过一段滑行后从斜坡上的O点水平飞出,斜坡与水平面的夹角θ=37°,运动员连同滑雪板的总质量m=50kg,他落到了斜坡上的A点,A点与O点的距离s=12m,如图14所示。忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10m/s2。
(sin37°=0.60;cos37°=0.80)
(1)运动员在空中飞行了多长时间?
(2)求运动员离开O点时的速度大小。
(3)运动员落到斜坡上顺势屈腿以缓冲,使他垂直于斜坡的速度在t=0.50s的时间内减小为零,设缓冲阶段斜坡对运动员的弹力可以看作恒力,求此弹力的大小。
排球网高H,半场长L,运动员扣球点高h,扣球点离网水平距离s、求:要使水平扣出的球既不触网、又不出界,扣球速度的取值范围应是多少?
一个高出地面为h的圆形平台,其半径为r,一根长为r的细线一端系在平台的中心,另一端系一个小球绕中心做圆周运动,线所能承受的最大张力为T.当小球运动逐渐加快,使细线断开后,小球落向地面.求小球落地点的位置.
遥控赛车比赛中有一个规定项目:飞越“壕沟”。比赛要求:赛车从起点A由静止出发,沿水平直线轨道运动,在B点飞出后越过“壕沟”,落到平观EF段(如图所示)。赛车通电后以额定功率P=1.5W工作,在AB段运动过程中,受到阻力恒为F1=0.3N,在空中运动的过程不计空气阻力。已知赛车质量m=0.1kg,AB的长度L=10.00m,BE的高度差h=1.25m,BE的水平距离s=1.50m。(重力加速度g=10m/s2).
(1)若赛车在AB轨道上能达到最大速度 ,求
,求 的大小;
的大小;
(2)要使赛车完成比赛,赛车通电时间至少为多长?
如图所示,在半径为R,质量分布均匀的某星球表面,有一倾角为
|
的斜坡。以初速度v0向斜坡水平抛出一个小球。测得经过时间t,小球垂直落在斜坡上的C点。求:
(1)小球落到斜坡上时的速度大小v;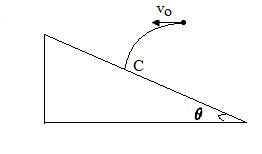
如图所示,摩托车做特技表演时,以v0=10m/s的初速度冲向高台,然后从高台水平飞出。若摩托车冲向高台的过程中以P=1.8kW的额定功率行驶,冲到高台上所用时间t=16s,人和车的总质量m=1.8×102kg,台高h=5.0m,摩托车的落地点到高台的水平距离s=7.5m。不计空气阻力,取g=10m/s2。求:
(1)摩托车从高台飞出到落地所用时间;
(2)摩托车落地时速度的大小;
(3)摩托车冲上高台过程中克服阻力所做的功。




⑴物品在下落的过程中,物品的重力势能变化了多少?
⑵物品在下落的过程中,重力的平均功率为多少?
⑶物品落地时重力的瞬时功率为多少?
如图所示,在距水平地面高h=0.80m的水平桌面一端的边缘放置一个质量m=0.80kg的木块B,桌面的另一端有一块质量M=1.0kg的木块A以初速度v0=4.0m/s开始向着木块B滑动,经过时间t=0.80s与B发生碰撞,碰后两木块都落到地面上。木块B离开桌面后落到地面上的D点。设两木块均可以看作质点,它们的碰撞时间极短,且已知D点距桌面边缘的水平距离s=0.60m,木块A与桌面间的动摩擦因数μ=0.25,重力加速度取g=10m/s2。求:

(1)两木块碰撞前瞬间,木块A的速度大小;
(2)木块B离开桌面时的速度大小;
(3)木块A落到地面上的位置与D点之间的距离。