高中物理平抛运动试题

某游戏装置放在竖直平面内，如图所示，装置由粗糙抛物线形轨道AB和光滑的圆弧轨道BCD构成，控制弹射器可将穿在轨道上的小球以不同的水平初速度由A点射入，最后小球将由圆轨道的最高点D水平抛出，落入卡槽中得分，圆弧半径为R，O′为圆弧的圆心，C为圆弧轨道最低点，抛物线轨道上A点在坐标轴的原点O上，轨道与圆弧相切于B点，抛物线轨道方程为y=ax²（0＜a＜），∠BO′C=θ，x轴恰好将半径O′D分成相等的两半，交点为P，x轴与圆弧交于Q点，则：   

（1）将小球以某一初速度水平由A点射入轨道，小球沿轨道运动到与A等高处Q，速度减为0，试求小球运动到B点的速度；
（2）由（1）得到的B点的速度，能否求出小球在A点射入的速度，如果能请求出v₀，不能，请说明理由（3）试求在多次弹射小球的过程中，机械能损失最小的一次，小球在最高点D对轨道的作用力与最低点C对轨道的作用力的比值．

某人站在高60 m的平台边缘，以20 m/s的初速度竖直向上抛出一石块，不考虑空气阻力，取g="10" m/s²求：
（1）石块上升的最大高度。
（2）石块从抛出到落地的时间。
（3）石块落到地面时的速度。

如图所示，在水平地面上固定一倾角θ＝37°、表面光滑的斜面体，物体A以v₁＝6 m/s的初速度沿斜面上滑，同时在物体A的正上方，有一物体B以某一初速度水平抛出，如果当A上滑到最高点时恰好被B物体击中．（A、B均可看做质点，sin 37°＝0.6，cos 37°＝0.8，重力加速度g取10 m/s²） 求：

（1）物体A上滑到最高点所用的时间t；
（2）物体B抛出时的初速度v₂；
（3）物体A、B间初始位置的高度差h.

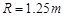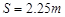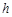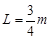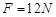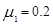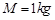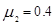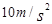如图所示，四分之一圆轨道OA与传送带相切相连，下方的CD水平轨道与他们在同一竖直面内。圆轨道OA的半径，传送带长，圆轨道OA光滑，AB与CD间的高度差为。一滑块从O点静止释放，当滑块经过B点时（无论传送带是否运动），静止在CD上的长为的木板（此时木板的末端在B点的正下方）在的水平恒力作用下启动，此时滑块落入木板中，已知滑块与传送带的摩擦因数，木板的质量，木板与CD间的摩擦因数为，取，求：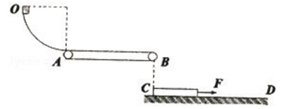

（1）如果传送带静止，求滑块到达B点的速度。
（2）如果传送带静止，求的取值范围。
（3）如果传送带可以以任意速度传动，取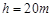，试判断滑块还能否落在木板上。

如图所示，小球从A点以固定的初速度v₀水平抛出，空气阻力不计，A点右下方有一带挡板的轮子，轮子与小球运动轨迹在同一竖直面内。轮子的半径为R，抛出点A比轮轴高h，挡板的初位置在与轮轴等高的B点，调整轮轴O的位置，使平抛轨迹与轮缘相切于C，OC与OB间夹角为θ角。求：

(l)小球抛出的初速度v₀大小为多少；
(2)小球抛出的瞬间轮子开始顺时针匀速转动，若不计挡板大小，要使小球打在挡板上，轮子转动的角速度为多少？

如图所示，墙壁上落有两只飞镖，它们是从同一位置水平射出的。飞镖A与竖直墙壁成α角，飞镖B与竖直墙壁成β角，两者相距为d，假设飞镖的运动是平抛运动，求：

（1）射出点离墙壁的水平距离；
（2）若在该射出点水平射出飞镖C，要求它以最小动能击中墙壁，则C的初速度应为多大？
（3）在第（2）问情况下，飞镖C与竖直墙壁的夹角多大？射出点离地高度应该满足什么条件？

如图所示是利用电力传送带装运麻袋包的示意图．传送带长l＝20 m，倾角θ＝37°，麻袋包与传送带间的动摩擦因数μ＝0.8，传送带的主动轮和从动轮半径R相等，传送带不打滑，主动轮顶端与货车底板间的高度差为h＝1.8 m，传送带匀速运动的速度为v＝2 m/s.现在传送带底端（传送带与从动轮相切位置）由静止释放一只麻袋包（可视为质点），其质量为100 kg，麻袋包最终与传送带一起做匀速运动，到达主动轮时随轮一起匀速转动．如果麻袋包到达主动轮的最高点时，恰好水平抛出并落在车厢底板中心，重力加速度g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8，求：

（1）主动轮的半径R；
（2）主动轮轴与货车车厢底板中心的水平距离x
（3）麻袋包在传送带上运动的时间t；

在如图所示的平面直角坐标系内，x轴水平、y轴竖直向下。计时开始时，位于原点处的沙漏由静止出发，以加速度a沿x轴匀加速度运动，此过程中沙从沙漏中漏出，每隔相等的时间漏出相同质量的沙。已知重力加速度为g，不计空气阻力以及沙相对沙漏的初速度。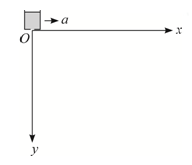

（1）求t₀时刻漏出的沙在t（t> t₀）时刻的位置坐标；
（2）t时刻空中的沙排成一条曲线，求该曲线方程。

如图所示，轨道ABCD的AB段为一半径R=0.2的光滑1/4圆形轨道，BC段为高为h=5的竖直轨道，CD段为水平轨道。一质量为0.1的小球由A点从静止开始下滑到B点时速度的大小为2/s，离开B点做平抛运动（g取10/s²），求：

①小球离开B点后，在CD轨道上的落地点到C的水平距离；
②小球到达B点时对圆形轨道的压力大小？
③如果在BCD轨道上放置一个倾角＝45°的斜面（如图中虚线所示），那么小球离开B点后能否落到斜面上？如果能，求它第一次落在斜面上的位置。

如图所示，质量为m＝0.2kg的小球（可视为质点）从水平桌面右端点A以初速度v₀水平抛出，桌面右侧有一竖直放置的光滑轨道MNP，其为半径R＝0.8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径.P点到桌面的竖直距离为R.小球飞离桌面后恰由P点无碰撞地落入圆轨道，取g＝10 m/s².

（1）求小球在A点的初速度v₀及AP间的水平距离x;
（2）求小球到达圆轨道最低点N时对N点的压力;
（3）判断小球能否到达圆轨道最高点M.

轻质弹簧原长为2l，将弹簧竖直放置在地面上，在其顶端将一质量为5m的物体由静止释放，当弹簧被压缩到最短时，弹簧长度为l．现将该弹簧水平放置，一端固定在A点，另一端与物块P接触但不连接．AB是长度为5l的水平轨道，B端与半径为l的光滑半圆轨道BCD相切，半圆的直径BD竖直，如图所示．物块P与AB间的动摩擦因数 $\mu =0.5$ ．用外力推动物块P，将弹簧压缩至长度l，然后释放，P开始沿轨道运动，重力加速度大小为g．

①若P的质量为m，求P到达B点时速度的大小，以及它离开圆轨道后落回到AB上的位置与B点间的距离；

②若P能滑上圆轨道，且仍能沿圆轨道滑下，求P得质量的取值范围．

如图所示，质量为M＝1kg，长为L＝2.7m的木板，其上表面光滑且距离水平地面的高度为h＝0.2m，在水平面上向右做直线运动，A、B是其左右两个端点．当木板的速度v₀＝4m/s时对木板施加一个大小为3N的水平向左的恒力F，并同时将一个质量为m＝1kg的小球轻放在木板上的P点（小球可视为质点，放在P点时相对于地面的速度为零)，PB＝，经过一段时间，小球从木板脱离后落到地面上．已知木板与地面间的动摩擦因数μ=0.1，g取10m/s².求：
（1)小球从放到木板上开始至落到地面所用的时间；
（2)小球落地瞬间木板的速度．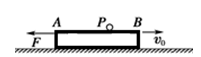

如图所示，下端封闭、上端开口、内壁光滑的细玻璃管竖直放置，管底有一带电的小球。整个装置水平匀速向右运动，垂直于磁场方向进入方向水平的匀强磁场，由于外力的作用，玻璃管在磁场中的速度保持不变，最终小球从上端口飞出，则从进入磁场到小球飞出端口前的过程中（   ）

A．小球带正电荷	B．小球做类平抛运动
C．洛仑兹力对小球做正功	D．管壁的弹力对小球做正功

如图所示，小球 a 从倾角为θ = 60°的固定粗糙斜面顶端以速度 v ₁沿斜面恰好匀速下滑，同时将另一小球 b 在斜面底端正上方与 a 球等高处以速度 v ₂ 水平抛出，两球恰在斜面中点 P 相遇，则下列说法正确的是(         )

A．v 1 : v 2 =" 2" : 1

B．v 1 : v 2 =" 1" : 1

C．若小球 b 以 2v 2水平抛出，则两小球仍能相遇

D．若小球 b 以 2v 2水平抛出，则 b 球落在斜面上时，a 球在 b球的下方

如图所示，半径R=0.6m的光滑圆弧轨道BCD与足够长的粗糙轨道DE在D处平滑连接，O为圆弧轨道BCD的圆心，C点为圆弧轨道的最低点，半径OB、OD与OC的夹角分别为53°和37°。将一个质量m=0.5kg的物体(视为质点)从B点左侧高为h=0.8m处的A点水平抛出，恰从B点沿切线方向进入圆弧轨道。已知物体与轨道DE间的动摩擦因数=0.8，重力加速度g取10m/s²，sin37°="0." 6，cos37°=0.8。求：

（1）物体水平抛出时的初速度大小v₀；
（2）物体在轨道DE上运动的路程s。