高中物理平抛运动试题

如图所示，从倾角为θ的足够长的斜面顶端p以速度V抛出一个小球，落在斜面上某处Q点，小球落在斜面上的速度与斜面的夹角α，若把初速度变为2V，则：(   )

A．空中的运动时间变为原来2倍

B．夹角α将变大

C．PQ间距一定大于原来间距的3倍

D．夹角α与初速度大小无关

如右图所示，在高处以初速度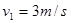水平抛出一个带刺飞镖，在离开抛出点水平距离l、2l处有A、B两个小气球以速度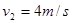匀速上升，先后被飞标刺破（认为飞标质量很大，刺破气球不会改变其平抛运动的轨迹），已知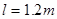。则飞标刺破A气球时，飞标的速度大小为  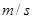      ；A、B两个小气球未被刺破前的匀速上升过程中，高度差      。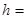

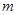如图所示，水平传送带以一定速度匀速运动，将质量m=1kg的小物块轻轻放在传送带上的P点，物块运动到A点后被水平抛出，小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑．B、C为圆弧上的两点，其连线水平，已知圆弧对应圆心角，A点距水平面的高度h=0.8m．小物块到达C点时的速度大小与B点相等，并沿固定斜面向上滑动，小物块从C点到第二次经过D点的时间间隔为0.8s，已知小物块与斜面间的动摩擦因数，重力加速度g取10 m/s²，取，cos53°=0.6，求：

（1）小物块从A到B的运动时间；
（2）小物块离开A点时的水平速度大小；
（3）斜面上C、D点间的距离．

如图所示，长木板固定在水平实验台上，在水平实验台右端地面上竖直放有一粗糙的被截去八分之三(即圆心角为135°)的圆轨道，轨道半径为R；放置在长木板A处的小球(视为质点)在水平恒力F的作用下向右运动，运动到长木板边缘B处撤去水平恒力F，小球水平抛出后恰好落在圆轨道C处，速度方向沿C处的切线方向，且刚好能到达圆轨道的最高点D处．已知小球的质量为m，小球与水平长木板间的动摩擦因数为μ，长木板AB长为L， B、C两点间的竖直高度为h，求：
(1)B、C两点间的水平距离x
(2)水平恒力F的大小
(3)小球在圆轨道上运动时克服摩擦力做的功

如图所示AB为半径R=1m四分之一光滑绝缘竖直圆弧轨道，在四分之一圆弧区域内存在着E=1×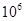V/m竖直向上的匀强电场，有一质量m=lkg带电量q=1.4×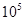C正电荷的物体（可视为质点），从A点的正上方距离A点H处由静止开始自由下落（不计空气阻力），BC段为长L=2m，与物体动摩擦因素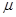=0.2的粗糙绝缘水平面，CD段为倾角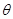=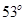且离地面DE高h=0.8m的斜面。求：
(1)若H=1m，物体能沿轨道AB到达最低点曰，求它到达B点时对轨道的压力大小？
(2)通过你的计算判断：是否存在某一H值，能使物体沿轨道AB经过最低点B后最终停在距离B点0.8m处？
(3)若高度H满足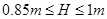：，请通过计算标示出物体从C处射出后打到的范围。（已知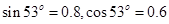。不需要计算过程，但要具体的位置。不讨论物体的反弹以后的情况。）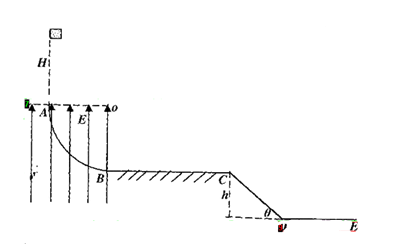

小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质
量为m的小球，甩动手腕，使球在竖直平面内做圆周运动，当球某次运动到最低点时，绳突然断掉．球飞离水平距离d后落地，如图341所示，已知握绳的手离地面高度为d，手与球之间的绳长为d，重力加速度为g，忽略手的运动半径和空气阻力。
(1)求绳断时球的速度大小v1，和球落地时的速度大小v2；
(2)问绳能承受的最大拉力多大？
(3)改变绳长，使球重复上述运动．若绳仍在球运动到最低点时断掉，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？

质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点，随传送带运动到A点后水平抛出，小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑的圆孤轨道下滑。B、C为圆弧的两端点，其连线水平。已知圆弧半径R=1.0m圆弧对应圆心角，轨道最低点为O，A点距水平面的高度h=0.8m,小物块离开C点后恰能无碰撞的沿固定斜面向上运动，0.8s后经过D点，物块与斜面间的动摩擦因数为= (g=10m/s²,sin37°=0.6,cos37°=0.8）试求：

（1）小物块离开A点时的水平初速度v₁ 。
（2）小物块经过O点时对轨道的压力。 
（3）假设小物块与传送带间的动摩擦因数为0.3，传送带的速度为5m/s，则PA间的最小距离是多少？
（4）斜面上CD间的距离。  

横截面为直角三角形的两个相同斜面如图紧靠在一起，固定在水平面上，它们的竖直边长都是底边长的一半。小球从左边斜面的顶点以不同的初速度向右平抛，最后落在斜面上。其中有三次的落点分别是a、b、c。下列判断正确的是（    ）

A．图中三小球比较，落在a的小球飞行时间最短

B．图中三小球比较，落在c的小球飞行过程速度变化最大

C．图中三小球比较，落在a的小球飞行过程速度变化最快

D．无论小球抛出时初速度多大，落到两个斜面上的瞬时速度都不可能与斜面垂直

如图所示，质量为m=0.2kg的小球（可视为质点）从水平桌面左端点A以初速度v₀水平抛出，桌面右侧有一竖直放置的光滑轨道MNP，其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径。P点到桌面的竖直距离也为R。，g=10m/s²，小球飞离桌面后恰由P点无碰撞地落入圆轨道

求：（1）小球在A点的初速度v₀及AP间水平距离x；
（2）小球到达圆轨道最低点N时对N点的压力；
（3）判断小球能否到达圆轨道最高点M。

如图所示，光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接。在过圆心O的水平界面的下方分布有水平向右的匀强电场。现有一个质量为m、电量为+q的小球从水平轨道上的A点由静止释放，小球运动到C点离开圆轨道后，经界面MN上的P点进入电场（P点恰好在A点的正上方，小球可视为质点，小球运动到C之前电量保持不变，经过C点后电量立即变为零）。已知A、B间的距离为2R，重力加速度为g。在上述运动过程中，

α

D

求：①电场强度E的大小;
②小球在圆轨道上运动时的最大速率；
③小球对圆轨道的最大压力。

现在的水上乐园,让年青人娱乐无穷,很多在设计时都巧妙利用了物理原理.如图为其中的一种娱乐活动示意图。其中MN为平直轨道，轨道上装有一竖直杆，竖直杆在电动机带动下能从M点沿水平方向做初速度为零、加速度为的匀加速直线运动(M点与平台竖直边缘相齐)，运动中杆始终竖直。上有防滑海绵的转盘漂浮于水面, 可随中心的转轴转动，转盘的角速度为1rad/s，转盘的转轴中心离平台的水平距离为L=8.09m。小玲（为计算简单,小玲大小不计视为质点）从离转盘高为H=3.2m的平台边缘抓住竖直杆，可随竖直杆一起运动。假设小玲落到转盘上时相对转盘的速度瞬间减为零， 已知小玲质量为m=50Kg，转盘半径为R=2m,(最大静摩擦力等于滑动摩擦力, 重力加速度为)。求：
（1）为保证小玲落在转盘的任何位置都不会被甩下，小玲与转盘间的动摩擦因数至少多大？
（2）为了能安全落在转盘上，那么小玲必须在出发后距M点多远的P点松手？

如图所示，一个质量为m的质点以速度从A点水平射出，以速度经过B点，不计空气阻力，则下列正确的说法是 ［ 　  ］

A．若质点以速度-从B点射出，它将刚好以速度-经过A点．

B．若质点以大于的速度从B点射出，它也有可能经过A点．

C．若质点以小于的速度从B点射出，它也有可能经过A点．

D．若质点以速度-从B点射出时还受到竖直向上大小为2 mg 的恒力，则它将刚好以速度-经过A点．

如图所示，一物体自倾角为的固定斜面顶端沿水平方向抛出后落在斜面上．物体与斜面接触时速度与水平方向的夹角满足                （）

A．		B．
C．		D．

一水平抛出的小球落到一倾角为的斜面上时，其速度方向与斜面垂直，运动轨迹如右图中虚线所示。小球在竖直方向下落的距离与在水平方向通过的距离之比为（）

A．		B．
C．		D．

湖南省电视台“智勇大冲关”游乐节目中，选手需要借助悬挂在高处的绳飞越到水面的浮台上，小明和小阳观看后对此进行了讨论。如图（13）所示，他们将选手简化为质量m=60kg的质点，选手抓住绳子末端由静止开始摆动，此时绳与竖直方向夹角=53°，绳长l=2m的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。取g=10m／s²(sin53^o=0.8,cos53^o=0.6)。求：

选手摆到最低点时对绳拉力的大小F；
选手摆到右边最高点时松手，选手将做什么运动？设水对选手的平均浮力，平均阻力，求选手落入水中的深度；
若要求选手摆到最低点时松手，且运动到浮台处离岸水平距离最大，则选手应将手握住绳子上离O点多长处？