在如图所示的四幅图中，AB.BC均为轻质杆，各图中杆的A.C端都通过铰链与墙连接，两杆都在B处由铰链相连接，下列说法正确的是（）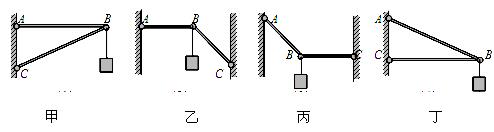
A.图中的AB杆可以用与之等长的轻绳代替的有甲、乙
B.图中的AB杆可以用与之等长的轻绳代替的有甲、丙、丁
C.图中的BC杆可以用与之等长的轻绳替代的有乙、丙
D.图中的BC杆可以用与之等长的轻绳代替的有乙、丁
如图所示，细绳下悬挂一小球D，小球与光滑的静止斜面接触，且细绳处于竖直状态，则下列说法中正确的是（）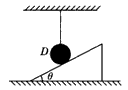
| A．斜面对D的支持力垂直于斜面向上 |
| B．D对斜面的压力竖直向下 |
| C．D与斜面间无相互作用力 |
| D．因D的质量未知，所以无法判定斜面对D支持力的大小和方向 |
如图所示，重物的质量为m，轻细绳AO的A端和BO的B端固定，平衡时AO水平，BO与水平方向的夹角为60°．AO的拉力F1和BO的拉力F2与物体重力的大小关系是（）
| A．F1＞mg | B．F1＜mg | C．F2＜mg | D．F2＞mg |
如图所示，为杂技表演的安全网示意图，网绳的结构为正方形，0、A.C.d…h为网绳的结点，安全网水平张紧后，若质量为
的运动员从高处落下，并恰好落在O点上，该处下凹至最低点时，网绳
、
构成
向上的张角，此时O点受到的向下冲击力大小为F，则这时O点周围每根网绳承受的力的大小为（）
A.F B.
C.
D.
如图所示，a，b，c三根绳子完全相同，其中b绳水平，c绳下挂一重物．若使重物加重，则这三根绳子中最先断的是（）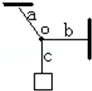
| A．a绳 | B．b绳 | C．c绳 | D．无法确定 |
如图所示，重物G用OA和OB两段等长的绳子悬挂在半圆弧的架子上，B点固定不动，A端由顶点C沿圆弧缓慢向D移动，在此过程中，绳子OA上的张力将（）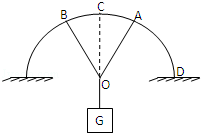
| A．变小 | B．变大 | C．先变大后变小 | D．先变小后变大 |
如图所示，小强用与水平方向成θ角的轻绳拉木箱，未拉动，此时绳中拉力为F，则木箱所受摩擦力的大小为 （）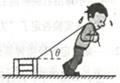
| A．Fcosθ | B．Fsinθ | C．0 | D．F |
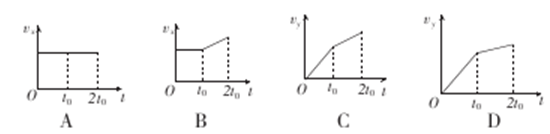
滑雪者从山上M处以水平速度飞出，经to时间落在山坡上N处时速度方向刚好沿斜坡向下，接着从N沿直线自由滑下，又经t0时间到达坡底 P处。斜坡NP与水平面夹角为30°，不计摩擦阻力和空气阻力，则从M到P过程中水平、竖直两方向的分速度νx、νy随时间变化的图象是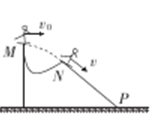
如图所示，质量M=
的木块A套在水平杆上，并用轻绳将木块：A与质量m=
的小球相连。今用跟水平方向成α=30o角的力F=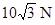
，拉着球带动木块一起向右匀速运动，运动中M、m相对位置保持不变，取g=10m/s 2。求：
（1）运动过程中轻绳与水平方向夹角θ；
（2）木块与水平杆间的动摩擦因数为μ。
将10N的力分解为两个分力F1、F2，F1、F2的值不可能是下列的哪一组
| A．F1=6N，F2=3N | B．F1=12N，F2=3N |
| C．F1=F2=10N | D．F1=F2=20N |
如图，老鹰沿虚线MN 斜向下减速俯冲的过程中，空气对老鹰的作用力可能是图中的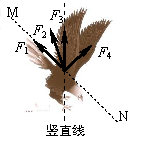
| A．F1 |
| B．F2 |
| C．F3 |
| D．F4 |
如图所示，质量均可忽略的轻绳与轻杆承受弹力的最大值一定，轻杆A端用铰链固定，滑轮在A点正上方（滑轮大小及摩擦均可不计），轻杆B端吊一重物G，现将绳的一端栓在杆的B端，用拉力F将B端缓慢上拉（均未断），在AB杆达到竖直前，以下分析正确的是（）
| A．绳子越来越容易断 | B．绳子越来越不容易断 |
| C．AB杆越来越容易断 | D．AB杆越来越不容易断 |
如图所示，细而轻的绳两端，分别系有质量为mA、mB的球，mA静止在光滑半球形表面P点（球可视为质点），已知过P点的半径与水平面夹角为60°，则mA和mB的关系是（）
| A．mA=mB | B．mA= mB |
C．mA=2mB | D．mB=mA |
为
，其中力
为
，那么另一个力
的大小可能是（）
粤公网安备 44130202000953号