如图所示,一轻绳的两端分别固定在不等高的A、B两点,现用另一轻绳将一物体系于O点,设轻绳AO、BO相互垂直, ,且两绳中的拉力分别为
,且两绳中的拉力分别为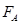 、
、 ,物体受到的重力为G,下列表述正确的是
,物体受到的重力为G,下列表述正确的是
A.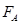 一定大于G
一定大于G
B.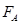 一定大于
一定大于
C.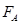 一定小于
一定小于
D.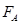 与
与 大小之和一定等于G
大小之和一定等于G
如图所示,用水平拉力 将小球缓慢地向右拉,细绳AB的拉力大小为
将小球缓慢地向右拉,细绳AB的拉力大小为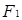 ,细绳CB的拉力大小为
,细绳CB的拉力大小为 ,细绳BD的拉力大小为
,细绳BD的拉力大小为 ,关于
,关于 、
、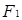 、
、 、
、 大小变化正确的是()
大小变化正确的是()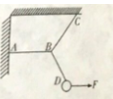
A. 变大 变大 |
B.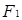 变小 变小 |
C. 不变 不变 |
D. 不变 不变 |
如图所示,一只重为G的松鼠站在倾斜角为θ的树枝上,则树枝对松鼠的作用力为()
| A.Gsinθ | B.Gcosθ | C.大于G | D.G |
如图为某同学设计的一个小实验.他将细绳的一端系在手指上(B处),绳的另一端系在直杆的A端,杆的另一端C顶在掌心上,组成一个“三角支架”.在杆的A端悬挂不同重物,并保持静止.通过实验会感受到()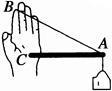
| A.绳子是被拉伸的,杆是被压缩的 |
| B.杆对手掌施加作用力的方向沿杆由C指向A |
| C.绳对手指施加作用力的方向沿绳由B指向A |
| D.所挂重物质量越大,绳和杆对手的作用力也越大 |
将一个力F分解为两个分力F1和F2,则下列说法中正确的是
| A.F是物体实际受到的力 |
| B.F1和F2两个分力在效果上可以取代力F |
| C.物体受到F1、F2和F三个力的作用 |
| D.F是F1和F2的合力 |
通过两个定滑轮,用两根细线去拉伸一根一端固定在墙上的橡皮筋OP。过滑轮A的线上挂上三个钩码,过滑轮B的线上挂上四个钩码,两根细线都接在橡皮筋的P端,在两个拉力的共同作用下,使橡皮筋从P点水平地拉伸到 点,此时两根细线间夹角为90°,如图所示,如果改用一根细线,绕过一只滑轮,要取得同样的效果,滑轮必须安装在_________,挂上____________个钩码
点,此时两根细线间夹角为90°,如图所示,如果改用一根细线,绕过一只滑轮,要取得同样的效果,滑轮必须安装在_________,挂上____________个钩码
三个相同的支座上分别搁着三个质量和直径都相等的光滑圆球a、b、c,支点P、Q在同一水平面上,a球的重心Oa位于球心,b球和c球的重心Ob、Oc分别位于球心的正上方和正下方,如图所示.三个球处于平衡状态,支点P对a球的弹力为Fa,对b球和c球的弹力分别为Fb和Fc。则()
| A.Fa=Fb=Fc | B.Fb>Fa>Fc | C.Fb<Fa<Fc | D.Fa>Fb=Fc |
右图是骨折病人的牵引装置示意图,绳的一端固定,绕过定滑轮和动滑轮后挂着一个重物,与动滑轮相连的帆布带拉着病人的脚,整个装置在同一竖直平面内.为了使脚所受的拉力增大,可采取的方法是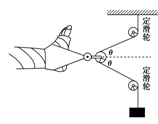
| A.只增加绳的长度 |
| B.只增加重物的质量 |
| C.只将病人的脚向左移动 |
| D.只将两定滑轮的间距减小 |
两个力F1和F2间的夹角为θ,两个力的合力为F.以下说法正确的是()
| A.若F1和F2大小不变,θ角越小,合力F就越小 |
| B.合力F总比分力中的任何一个力都大 |
| C.如果夹角θ不变,F1大小不变,只要F2增大,合力F就必然增大 |
| D.合力F可能比分力中的任何一个力都小 |
如图所示,用三根轻绳将质量均为m的A、B两小球及水平天花板上的固定O两两连接,然后用一水平方向的力F作用于A球上,此时三根轻绳均处于伸直状态,且OB绳恰好处于竖直方向,两球均处于静止状态,三根轻绳长度之比为OA:AB:OB=3:4:5,试计算OA绳拉力及F的大小。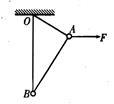
如图所示,斜面顶端固定有半径为R的轻质滑轮,用不可伸长的轻质细绳将半径为r的球沿斜面缓慢拉升。不计各处摩擦,且R>r。设绳对球的拉力为F,斜面对球的支持力为N,则关于F和N的变化情况,下列说法正确的是()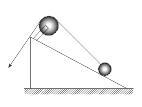
| A.F一直增大,N一直减小 |
| B.F一直增大,N先减小后增大 |
| C.F一直减小,N保持不变 |
| D.F一直减小,N一直增大 |
如图所示,物块M通过与斜面平行的细绳跨过定滑轮与小物块m相连,当斜面的倾角θ改变时,下列关于物块M所受摩擦力大小判断正确的是()
| A.若物块M保持静止,则θ角越大,摩擦力越大 |
| B.若物块M保持静止,则θ角越大,摩擦力越小 |
| C.若物块M沿斜面下滑,则θ角越大,摩擦力越大 |
| D.若物块M沿斜面下滑,则θ角越大,摩擦力越小 |