如图所示,用绳AC和BC吊起一重物,绳与竖直方向夹角分别为30°和60°,AC绳能承受的最大拉力为150N,而BC绳能承受的最大的拉力为100N,求物体最大重力不能超过多少?
如图所示,用不可伸长的轻绳AC和BC吊起一质量不计的沙袋,绳AC和BC与天花板的夹角分别为60°和30°。现缓慢往沙袋中注入沙子,重力加速度 ,
,
(1)当注入沙袋中沙子的质量m=10kg时,求绳子AC和BC上的拉力大小 ;
;
(2)若AC能承受的最大拉力为150N,BC能承受的最大拉力为100N,为使绳子不断裂,求注入沙袋中沙子质量的最大值M
如图所示,物体的质量为2 kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围.
如图所示,一质量为m=100kg的箱子静止在水平面上,与水平面间的动摩擦因素为μ=0.5。现对箱子施加一个与水平方向成θ=37°角的拉力,经t1=10s后撤去拉力,又经t2=1s箱子停下来。sin37°=0.6,cos37°=0.8,g=10m/s2。求:
(1)拉力F大小;
(2)箱子在水平面上滑行的位移x。
如图是一种测定风力的仪器的原理图,一金属球固定在一细长的轻金属丝下端,能绕悬挂点O在竖直平面内转 动,无风时金属丝自然下垂,现发现水平风力大小为F时,金属丝偏离竖直方向的角度为θ,求:
(1)金属球对金属丝的拉力的大小;
(2)金属球的质量为多少?
用穿过钢管的绳索吊起钢管,钢管重1.8×104N,长2m厚度可略去不计,如图所示,绳索能承受的最大拉力为1.5×104N,绳索全长至少要多长?
将橡皮筋的一端固定在A点,另一端拴上两根细绳.每根细绳分别连着一个量程为5N,最小刻度为0.1N的弹簧测力计.沿着两个不同的方向拉弹簧测力计.当橡皮筋的活动端拉到O点时,两根细绳相互垂直,如图所示,这时弹簧测力计的读数可从图中读出.

(1)由图可读得两个相互垂直的拉力的大小分别为 N和 N.
(2)在方格纸上按作图法的要求画出这两个力及它们的合力.
(3)求其合力的大小.
如图所示,一足够长的固定光滑斜面倾角 =37°,两物块A、B的质量
=37°,两物块A、B的质量 1kg、
1kg、 4kg。两物块之间的轻绳长L=0.5m,轻绳可承受的最大拉力为T=12N,对B施加一沿斜面向上的力 F,使A、B由静止开始一起向上运动,力F逐渐增大, g取10m/s2(sin37°=0.6,cos37°=0.8)。
4kg。两物块之间的轻绳长L=0.5m,轻绳可承受的最大拉力为T=12N,对B施加一沿斜面向上的力 F,使A、B由静止开始一起向上运动,力F逐渐增大, g取10m/s2(sin37°=0.6,cos37°=0.8)。
(1)若某一时刻轻绳被拉断,求此时外力F的大小;
(2)若轻绳拉断瞬间A、B的速度为3m/s,绳断后保持外力F不变,求当A运动到最高点时,A、B之间的距离。
如图所示,半径为r=10cm、质量为M=1.8kg的均匀球靠竖直墙放置,左下方有一厚为h=4cm、质量为m=1kg的木块.(取g=10m/s2)
(1)若不计摩擦.用多大的水平力F推木块才能使球恰好离开地面?
(2)此时木块对地的压力?
足够长光滑斜面BC的倾角α=53°,小物块与水平面间的动摩擦因数μ=0.5,水平面与斜面之间B点有一小段弧形连接,一质量m=2kg的小物块静止于A点,现在AB段对小物块施加与水平方向成α=53°角的恒力F作用,如图(a)所示,小物块在AB段运动的速度--时间图像如图(b)所示,到达B点迅速撤去恒力F.(已知sin53°=0.8,cos53°=0.6,g取10m/s2),求: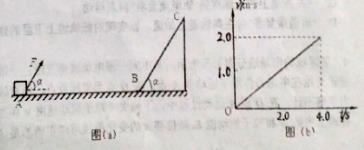
(1)小物块所受到的恒力F;
(2)小物块从B点沿斜面向上运动,到返回B点所用的时间;
(3)小物块能否返回到A点?若能,计算小物块通过A点时的速度:若不能,计算小物块停止运动时离B点的距离。
用细绳AO、BO吊一重物,两绳子能承受的最大力均为100N,绳与竖直方向夹角分别为30°和60°,如图所示.若使绳子不断,最多能悬挂多重的重物?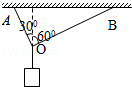
如图所示,用三根轻绳将质量均为m的A、B两小球及水平天花板上的固定O两两连接,然后用一水平方向的力F作用于A球上,此时三根轻绳均处于伸直状态,且OB绳恰好处于竖直方向,两球均处于静止状态,三根轻绳长度之比为OA:AB:OB=3:4:5,试计算OA绳拉力及F的大小。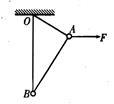
一条船由两岸纤夫拉着沿水平面的笔直水渠前进,水流作用可以忽略。岸这边纤夫以恒力 拉船,方向如图所示,那么,对岸纤夫朝什么方向拉船时,用力最小?最小值为多少?
拉船,方向如图所示,那么,对岸纤夫朝什么方向拉船时,用力最小?最小值为多少?