如图,半圆形支架BAD,两细绳OA和OB结于圆心O,下悬重为G的物体,使OA绳固定不动,将OB绳的B端沿半圆支架从水平位置逐渐移至竖直位置C的过程中,分析OA绳和OB绳所受的力大小如何变化?( )

| A.OA绳拉力逐渐变大 | B.OA绳拉力逐渐变小 |
| C.OB绳拉力先变小后变大 | D.OB绳拉力逐渐变小 |
如图所示,一定质量的物体通过轻绳悬挂,结点为O.人沿水平方向拉着OB绳,物体和人均处于静止状态.若人的拉力方向不变,缓慢向左移动一小段距离,下列说法正确的是( )

| A.OA绳中的拉力先减小后增大 |
| B.OB绳中的拉力不变 |
| C.人对地面的压力逐渐减小 |
| D.地面给人的摩擦力逐渐增大 |
一根轻质细绳能承受的最大拉力是G,现把一重为G的物体系在绳的中点,两手先并拢分别握住绳的两端,然后缓慢地左右对称分开,若想绳不断,两绳间的夹角不能超过( )
| A.45° | B.60° | C.120° | D.135° |
滑板运动是一项非常刺激的水上运动(如图所示),研究表明,在进行滑板运动时,水对滑板的作用力N垂直于板面,大小为 ,其中v为滑板速率(水可视为静止)。某次运动中,在水平牵引力F作用下,当滑板和水面的夹角
,其中v为滑板速率(水可视为静止)。某次运动中,在水平牵引力F作用下,当滑板和水面的夹角 =37°时,滑板做匀速直线运动,相应的k=40kg/m,人和滑板的总质量为80kg,(重力加速度
=37°时,滑板做匀速直线运动,相应的k=40kg/m,人和滑板的总质量为80kg,(重力加速度 ,sin37°=0.6,忽略空气阻力)。试求:
,sin37°=0.6,忽略空气阻力)。试求:
(1)水平牵引力F的大小;
(2)滑板的速率v=?
如图所示,可以视为质点的小球A.B球被轻绳连接后,挂在光滑的圆柱上恰好处于静止状态,已知圆心为O,∠AOB=90°,OB与竖直方向的夹角α=30°,则A.B球的质量之比为

A.1:2 B.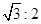 C.
C.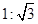 D.
D.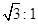
如图所示是山区村民用斧头劈柴的剖面图,图中BC边为斧头背,AB.AC边是斧头的刃面,要使斧头容易劈开木柴,则

A.BC边短些,AB边也短些 B.BC边长一些,AB边短一些
C.BC边短一些,AB边长一些 D.BC边长一些,AB边也长一些
如图所示,一个重60N的物体置于光滑的水平面上,当用一个F=20N的力竖直向上拉物体时,物体所受的合力为
| A.0 | B.40N,方向竖直向下 |
| C.40N,方向竖直向上 | D.80N,方向竖直向上 |
如图所示,小船过河时,船头偏向上游与水流方向成α角,船相对于静水的速度为v,其航线恰好垂直于河岸。现水流速度稍有增大,为保持航线不变,且准时到达对岸,下列措施中可行的是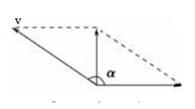
| A.减小α角,增大船速v |
| B.增大α角,增大船速v |
| C.减小α角,保持船速v不变 |
| D.增大α角,保持船速v不变 |
如图,用两根等长轻绳将木板悬挂在竖直木桩上等高的两点,制成一简易秋千。某次维修时将两轻绳各剪去一小段,但仍保持等长且悬挂点不变。木板静止时,F1表示木板所受合力的大小,F2表示单根轻绳对木板拉力的大小,则维修后
| A.F1不变,F2变大 |
| B.F1不变,F2变小 |
| C.F1变大,F2变大 |
| D.F1变小,F2变小 |
如图所示,欲使在固定的粗糙斜面上匀速下滑的木块A停下,可采用的方法是( )

| A.增大斜面的倾角 |
| B.对木块A施加一个竖直向向上但小于木块A重力的力 |
| C.对木块A施加一个竖直向下的力 |
| D.对木块A施加一个垂直于斜面向下的力 |
如图所示,将一根不能伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子张力为F1;将绳子B端移至C点,待整个系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F2;将绳子B端移至D点,待整个系统达到平衡时,两段绳子间的夹角为θ3,绳子张力F3,不计摩擦,则( )

A.θ1=θ2=θ3 B.θ1<θ2<θ3
C.F1<F2<F3 D.F1=F2<F3
如图所示,一质量均匀的实心圆球被直径AB所在的平面一分为二,先后以AB沿水平和竖直两种不同方向放置在光滑支架上,处于静止状态.忽略一切摩擦,两半球间的作用力分别为F和F’,已知支架间的距离为AB的一半,则 为
为
A. |
B. |
C. |
D. |
三个共点力的大小分别为F1=5N,F2=10N,F3=20N,则它们的合力最大值__________N,最小值____N,若F3=7N,则三力的最小值为_____N。