高中物理试题

地球同步卫星离地心距离为r,运行速度为v₁,加速度为a₁,地球赤道上的物体随地球自转的加速度为a₂,第一宇宙速度为v₂,地球半径为R,则以下正确的是(  )

A．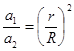

B．

C．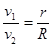

D．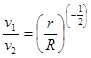

我们的银河系的恒星中大约四分之一是双星。某双星由质量不等的星体S₁和S₂构成，两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动。由天文观察测得其运动周期为T，S₁到C点的距离为r₁,S₁和S₂的距离为r，已知引力常量为G。由此可求出S₂的质量为（   ）

A．

B．

C．

D．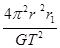

人用绳子通过定滑轮拉物体A，A穿在光滑的竖直杆上，当以速度v₀匀速地拉绳使物体A到达如图所示位置时，绳与竖直杆的夹角为θ，则物体A实际运动的速度是(  )

A．v0sinθ

B．

C．v0cosθ

D．

如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足(  )

A．tanφ=sinθ

B．tanφ=cosθ

C．tanφ=tanθ

D．tanφ=2tanθ

如图所示，AOB是由某种透明物质制成的圆柱体横截面（O为圆心），折射率为．今有一束平行光以45°的入射角射向柱体的OA平面，这些光线中有一部分不能从柱体的AB面上射出，设凡射到OB面的光线全部被吸收，也不考虑OA面的反射，求圆柱体AB面上能射出光线的部分占AB表面的几分之几．

一列横波在x轴上传播，在t₁＝0时刻波形如图中实线所示，t₂＝0．05 s时刻波形如图中虚线所示．求：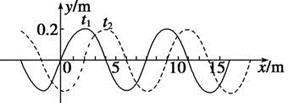

（1）这列波的振幅和波长；
（2）这列波的波速的大小和方向。

利用薄膜干涉可检查工件表面的平整度．如图（a）所示,现使透明标准板M和待检工件N间形成一楔形空气薄层,并用单色光照射,可观察到如图（b）所示的干涉条纹,条纹的弯曲处P和Q对应于A和B处,下列判断中正确的是（    ）

A．N的上表面A处向上凸起

B．N的上表面B处向上凸起

C．条纹的cd点对应处的薄膜厚度相同

D．条纹的d．e点对应处的薄膜厚度相同

一列简谐横波，在t=0．6s时刻的图像如下图甲所示，此时，P、Q两质点的位移均为 1cm，波上A质点的振动图像如图乙所示，则以下说法正确的是（     ）

A．这列波沿x轴正方向传播

B．这列波的波速是m/s

C．从t=0．6 s开始，紧接着的Δt=0．6 s时间内，A质点通过的路程是10m

D．从t=0．6 s开始，质点P比质点Q早回到平衡位置

如图所示，一束入射光AO从某种介质以入射角α射入空气，以O点为圆心，R₁为半径画圆C₁与折射光线OB交于M点，过M点向两介质的交界面作垂线与入射光线AO的延长线交于N点，以O点为圆心，ON为半径画另一个圆C₂，测得该圆的半径为R₂，下列判断正确的是（   ）

A．该介质的折射率为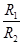

B．若光由介质射入空气发生全反射，则临界角为arcsin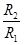

C．若过圆C1与界面的交点D作界面的垂线交圆C2于P点，则OP与法线所夹的锐角等于全反射的临界角

D．若入射光的强度保持不变，逐渐增大入射角α，则折射光的强度将逐渐增加

质点以坐标原点O为中心位置在y轴上做简谐运动，其振动图象如图甲所示，振动在介质中产生的简谐横波沿x轴正方向传播，波速为1．0 m/s。0．3s后，此质点立即停止运动，再经过0．1s后的波形图是图乙中的（   ）

光纤维通信是一种现代化的通信手段，它可以为客户提供大容量、高速度、高质量的通信服务，为了研究问题方便，我们将光导纤维简化为一根长直玻璃管，如图所示．设此玻璃管长为L，折射率为n．已知从玻璃管左端面射入玻璃内的光线在玻璃管的侧面上恰好能发生全反射，最后从玻璃管的右端面射出．设光在真空中的传播速度为c，则光通过此段玻璃管所需的时间为（   ）

A．	B．
C．	D．

如图所示，一细束白光通过玻璃三棱镜折射后分为各种单色光，取其中a．b．c三种色光，下列说法正确的是：（    ）

A．若b光为绿光，则c光可能为蓝光

B．若分别让a．b．c三色光通过一双缝装置，则a光形成的干涉条纹的间距最小

C．a．b．c三色光在玻璃三棱镜中的传播速度依次越来越小

D．若让a．b．c三色光以同一入射角，从某介质射向空气，b光恰能发生全反射，则c光也一定能发生全反射

现在高速公路上的标志牌都用“回归反光膜”制成，夜间行车时，它能把车灯射出的光逆向返回，所以标志牌上的字特别醒目。这种“回归反光膜”是用球体反射元件制作的。如图反光膜内部均匀分布着直径为10 μm的细玻璃珠，所用玻璃的折射率n=，为使入射的车灯光线经玻璃珠折射→反射→再折射后恰好和入射光线平行，第一次入射时的入射角i应是（    ）

A．15°

B．30°

C．45°

D．60°

如图所示，将一个小球水平抛出，抛出点距水平地面的高度h＝1.8m，小球抛出的初速度为。不计空气阻力。取。求：

（1）小球从抛出到落地经历的时间t；
（2）小球落地点与抛出点的水平距离x；
（3）小球落地时的速度大小v

如图所示，A.B为咬合转动的两个齿轮，它们的半径分别为和，且,则A.B两轮边缘上两点的角速度之比为=      ；线速度之比=   。