已知M是△ABC内的一点,且 ·
· =2
=2 ,∠BAC=30°,若△MBC,△MCA和△MAB的面积分别为
,∠BAC=30°,若△MBC,△MCA和△MAB的面积分别为 ,x,y,则
,x,y,则 +
+ 的最小值是( )
的最小值是( )
| A.20 | B.18 | C.16 | D.19 |
已知x+3y-1=0,则关于 的说法正确的是( )
的说法正确的是( )
| A.有最大值8 | B.有最小值 |
| C.有最小值8 | D.有最大值 |
下列结论正确的是( )
A.当x>0且x≠1时,lgx+ ≥2 ≥2 |
B.当x>0时, + + ≥2 ≥2 |
C.当x≥2时,x+ ≥2 ≥2 |
D.当0<x≤2时,x- 无最大值 无最大值 |
(能力提升)直线ax+by+c=0与圆x2+y2=9相交于两点M,N,若c2=a2+b2,则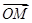 ·
·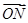 (O为坐标原点)等于( )
(O为坐标原点)等于( )
| A.-7 | B.-14 | C.7 | D.14 |
由直线y=x+1上的一点向圆(x-2)2+(y-1)2=1引切线,则切线长的最小值为
A. |
B.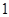 |
C. |
D. |
设a,b,c分别是△ABC中角A,B,C所对边的边长,则直线xsin A+ay+c=0与直线bx-ysin B+sin C=0的位置关系是( )
| A.平行 | B.重合 | C.垂直 | D.相交但不垂直 |
如果AC<0,且BC<0,那么直线Ax+By+C=0不通过( ).
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
直线x+2ay-1=0与(a-1)x+ay+1=0平行,则a等于( )
A. |
B. 或0 或0 |
C.0 | D.-2或0 |
已知直线 在
在 轴和
轴和 轴上的截距相等,则a的值是( )
轴上的截距相等,则a的值是( )
| A.1 | B.-1 | C.-2或-1 | D.-2或1 |
(能力提高)已知函数f(x)=x3+ax2+bx+c有两个极值点x1,x2.若f(x1)=x1<x2,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数为( )
| A.3 | B.4 | C.5 | D.6 |
当x∈[-2,1]时,不等式ax3-x2+4x+3≥0恒成立,则实数a的取值范围是( )
| A.[-5,-3] | B. |
| C.[-6,-2] | D.[-4,-3] |