高中数学选择题

记 S _n为等比数列{ a _n}的前 n项和．若 a ₅- a ₃=12， a ₆- a ₄=24，则 $\frac{S_n}{a_n}$ =（    ）

A．

2 ^n-1

B．

2-2 ^1- ^n

C．

2-2 ^n ^-1

D．

2 ^1- ^n-1

已知单位向量 $\vec{a}$ ， $\vec{b}$ 的夹角为60°，则在下列向量中，与 $\vec{b}$ 垂直的是（    ）

A．

$\vec{a}+2\vec{b}$

B．

$2\vec{a}+\vec{b}$

C．

$\vec{a}-2\vec{b}$

D．

$2\vec{a}-\vec{b}$

在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成1200份订单的配货，由于订单量大幅增加，导致订单积压.为解决困难，许多志愿者踊跃报名参加配货工作.已知该超市某日积压500份订单未配货，预计第二天的新订单超过1600份的概率为0.05，志愿者每人每天能完成50份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于0.95，则至少需要志愿者（    ）

A．

10名

B．

18名

C．

24名

D．

32名

如图，将钢琴上的12个键依次记为 a ₁， a ₂，…， a ₁₂.设1≤ i< j< k≤12．若 k- j=3且 j- i=4，则称 a _i， a _j， a _k为原位大三和弦；若 k- j=4且 j- i=3，则称 a _i， a _j， a _k为原位小三和弦．用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为（    ）

A．

5

B．

8

C．

10

D．

15

（1-i） ⁴=（    ）

A．	-4	B．	4
C．	-4i	D．	4i

已知集合 A={ x|| x|<3， x∈ Z}， B={ x|| x|>1， x∈ Z}，则 A∩ B=（    ）

A．	$\varnothing$	B．	{-3，-2，2，3）
C．	{-2，0，2}	D．	{-2，2}

在△ ABC中，cos C= $\frac{2}{3}$ ， AC=4， BC=3，则tan B=（    ）

A．

$\sqrt{5}$

B．

2 $\sqrt{5}$

C．

4 $\sqrt{5}$

D．

8 $\sqrt{5}$

下图为某几何体的三视图，则该几何体的表面积是（    ）

A．

6+4 $\sqrt{2}$

B．

4+4 $\sqrt{2}$

C．

6+2 $\sqrt{3}$

D．

4+2 $\sqrt{3}$

点(0，﹣1)到直线 $y=k\left(x+1\right)$ 距离的最大值为（    ）

A．

1

B．

$\sqrt{2}$

C．

$\sqrt{3}$

D．

2

设 $O$ 为坐标原点，直线 $x=2$ 与抛物线 C： $y^2=2\mathit{px}(p>0)$ 交于 $D$ ， $E$ 两点，若 $\mathit{OD}\perp \mathit{OE}$ ，则 $C$ 的焦点坐标为（    ）

A．

$\left(\frac{1}{4},0\right)$

B．

$\left(\frac{1}{2},0\right)$

C．

$(1,0)$

D．

$(2,0)$

设一组样本数据 x ₁， x ₂，…， x _n的方差为0.01，则数据10 x ₁，10 x ₂，…，10 x _n的方差为（    ）

A．

0.01

B．

0.1

C．

1

D．

10

若 $\bar{z}\left(1+i\right)=1-i$ ，则 z=（    ）

A．

1-i

B．

1+i

C．

-i

D．

i

已知集合 $A=\left\{1，2，3，5，7，11\right\}$ ， $B=\left\{x|3<x<15\right\}$ ，则 A∩ B中元素的个数为（    ）

A．

2

B．

3

C．

4

D．

5

下列各式的大小关系正确的是（ ）

A．sin11°＞sin168°

B．sin194°＜cos160°

C．cos（﹣）＞cos

D．tan（﹣）＜tan（﹣）

已知不共线向量，，=t﹣（t∈R），=2+3，若A，B，C三点共线，则实数t=（ ）

A．﹣

B．﹣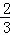

C．

D．﹣