一个正三棱锥的四个顶点都在半径为R的球面上,其中底面的三个顶点在该球的一个大圆上,且该正三棱锥的体积是 ,则球的体积为
,则球的体积为
A. |
B. |
C. |
D. |
正方形 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边 、
、 上,且
上,且 ,
, ,将此正方形沿
,将此正方形沿 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥 的体积是
的体积是
A. |
B. |
C. |
D. |
若正方体的棱长为 ,则以该正方体各个面的中心为顶点的凸多面体的体积为( )
,则以该正方体各个面的中心为顶点的凸多面体的体积为( )
A. |
B. |
C. |
D. |
设直线 与球
与球 有且只有一个公共点
有且只有一个公共点 ,从直线
,从直线 出发的两个半平面
出发的两个半平面 截球的两截面圆的半径分别为
截球的两截面圆的半径分别为 和
和 ,二面角
,二面角 的平面角为
的平面角为 ,则球
,则球 的表面积为
的表面积为
A.  |
B. |
C. |
D. |
某器物的三视图如图2所示,根据图中数据可知
该器物的表面积为
A. |
B. |
C. |
D. |

、如右图是一个简单空间几何体的三视图,其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是 ( )
( )
AB 4
C D
D
已知正方体的外接球的体积是 ,则这个正方体的棱长是
,则这个正方体的棱长是
A. |
B. |
C. |
D. |
圆台的轴截面面积是Q,母线与下底面成60°角,则圆台的内切球的表面积是()。
A.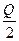 |
B.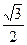 Q Q |
C.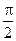 Q Q |
D.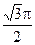 Q Q |
如图所示,已知球O为棱长为1的正方体ABCD—A1B1C1D1的内切球,则平面
ACD1截球O的截面面积为()
A. |
B. |
C. |
D. |
在棱锥 中,侧棱PA、PB、PC两两垂直,Q为底面
中,侧棱PA、PB、PC两两垂直,Q为底面 内一点,若点Q到三个侧面的距离分别为3、4、5,则以线段PQ为直径的球的表面积为()
内一点,若点Q到三个侧面的距离分别为3、4、5,则以线段PQ为直径的球的表面积为()
A.100 B.50
B.50 C.
C. D.
D.