已知矩形 的周长为
的周长为 ,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为.
,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为.
一个几何体的三视图如图所示,如该几何体的表面积为92 ,则
,则 的值为()
的值为()
| A.4 | B.5 | C.6 | D.7 |
一个几何体的三视图如图所示,那么该几何体的体积是()
A. |
B. |
C. |
D. |
一个几何体的三视图如图所示,那么该几何体的体积是()
A. |
B. |
C. |
D. |
一个几何体的三视图如右图所示,则该几何体的体积为()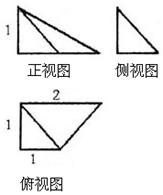
A.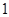 |
B.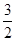 |
C.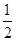 |
D.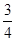 |
一个几何体的三视图如图所示,则这个几何体的外接球的体积为()
A. |
B. π π |
| C.2π | D. |
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,点
,点 是
是 的中点,点
的中点,点 是边
是边 上的任意一点.
上的任意一点.
(Ⅰ)当点 为
为 边的中点时,判断
边的中点时,判断 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)证明:无论点 在
在 边的何处,都有
边的何处,都有 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
已知 ,
, 平面
平面 ,若
,若 ,则四面体
,则四面体 的外接球(顶点都在球面上)的表面积为()
的外接球(顶点都在球面上)的表面积为()
A. |
B. |
C. |
D. |
半径为1的球面上有四个点A,B,C,D,球心为点O,AB过点O, ,
, ,
, , 则三棱锥
, 则三棱锥 的体积为()
的体积为()
A. |
B. |
C. |
D. |
已知四棱锥,它的底面是边长为 的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有个,该四棱锥的体积为.
的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有个,该四棱锥的体积为.

如图是一个几何体的三视图,根据图中的数据,计算该几何体的表面积为
A. |
B. |
C. |
D. |
如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足PD=PF=1,PE=2,则三棱锥P – DEF的体积是.