某同学在研究函数 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式 对
对 恒成立;
恒成立;
②函数 的值域为
的值域为 ;
;
③函数 为
为 上的单调函数;
上的单调函数;
④若 ,则一定有
,则一定有 ;
;
⑤函数 在
在 上有三个零点。
上有三个零点。
其中正确结论的序号有______________.(请将你认为正确的结论的序号都填上)
已知函数 对任意的
对任意的 满足
满足 ,且当
,且当 时,
时, .若
.若 有4个零点,则实数
有4个零点,则实数 的取值范围是 .
的取值范围是 .
下列命题中正确的是 .
①若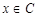 ,则方程
,则方程 只有一个根
只有一个根
②若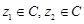 且
且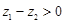 ,则
,则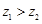
③若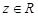 ,则
,则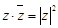 不成立
不成立
④若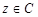 ,且
,且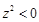 ,那么
,那么 一定是纯虚数
一定是纯虚数
设 若函数f(x)在区间(1,3)内有零点,则实数a的取值范围为 .
若函数f(x)在区间(1,3)内有零点,则实数a的取值范围为 .
下列说法:
①函数 的零点只有1个且属于区间
的零点只有1个且属于区间 ;
;
②若关于 的不等式
的不等式 恒成立,则
恒成立,则 ;
;
③函数 的图像与函数
的图像与函数 的图像有3个不同的交点;
的图像有3个不同的交点;
④函数 的最小值是1.
的最小值是1.
正确的有 .(请将你认为正确的说法的序号都写上)
定义在 上的函数
上的函数 满足:①当
满足:①当 时,
时, ;②
;② .设关于
.设关于 的函数
的函数 的零点从小到大依次为
的零点从小到大依次为 .若
.若 ,则
,则 ________ ;若
________ ;若 ,则
,则 ________________.
________________.