若函数 的一个正数零点附近的函数值用二分法计算,得数据如下:
的一个正数零点附近的函数值用二分法计算,得数据如下:
 |
 |
 |
 |
 |
 |
那么方程 的一个最接近的近似根为 ( )
的一个最接近的近似根为 ( )
(A) (B)
(B) (C)
(C) (D)
(D)
设 是定义在R上的偶函数,对χ
是定义在R上的偶函数,对χ ,都有
,都有 ,且当χ
,且当χ [-2,0]时,
[-2,0]时,
 ,若在区间(-2,6]内关于χ的方程
,若在区间(-2,6]内关于χ的方程 (
( >1)恰有3个不同的实数根,
>1)恰有3个不同的实数根,
则 的取值范围是( )
的取值范围是( )
| A.(1,2) | B.(2,+∞) | C.(1, ) ) |
D.( ,2) ,2) |
己知函数f(x)=|x-2|+1,g(x)= kx,若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围是
A.(0, ) ) |
B.( ,1) ,1) |
C.(1,2) | D.(2,+∞) |
函数f(x)="ln" (x +1) -  的一个零点所在的区间是( )
的一个零点所在的区间是( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
已知函数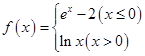 ,则下列关于函数
,则下列关于函数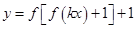 (
( )的零点个数的判断正确的是 ( )
)的零点个数的判断正确的是 ( )
A.当 时,有 时,有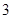 个零点;当 个零点;当 时,有 时,有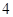 个零点 个零点 |
B.当 时,有 时,有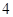 个零点;当 个零点;当 时,有 时,有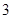 个零点 个零点 |
C.无论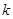 为何值,均有 为何值,均有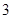 个零点 个零点 |
D.无论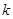 为何值,均有 为何值,均有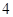 个零点 个零点 |