命题“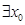 ∈N,x02 +2xo≥3”的否定为( )
∈N,x02 +2xo≥3”的否定为( )
A.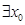 ∈N,x02 +2x0≤3 ∈N,x02 +2x0≤3 |
B. ∈N ,x2+2x≤3 ∈N ,x2+2x≤3 |
C.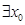 ∈N,x02 +2x0<3 ∈N,x02 +2x0<3 |
D. ∈N,x2+2x<3 ∈N,x2+2x<3 |
下列说法中,正确的是
A.命题“若 ,则 ,则 ”的否命题是假命题. ”的否命题是假命题. |
B.设 为两个不同的平面,直线 为两个不同的平面,直线 ,则 ,则 是 是  成立的充分不必要条件. 成立的充分不必要条件. |
C.命题“ ”的否定是“ ”的否定是“ ”. ”. |
D.已知 ,则“ ,则“ ”是“ ”是“ ”的充分不必要条件. ”的充分不必要条件. |
下列命题中,真命题是( )
| A.∃m∈R,使函数f(x)=x2+mx(x∈R)是偶函数 |
| B.∃m∈R,使函数f(x)=x2+mx(x∈R)是奇函数 |
| C.∀m∈R,函数f(x)=x2+mx(x∈R)都是偶函数 |
| D.∀m∈R,函数f(x)=x2+mx(x∈R)都是奇函数 |
下列命题中的假命题是( )
| A.∃x∈R,lgx=0 | B.∃x∈R,tanx=1 |
| C.∀x∈R,x3>0 | D.∀x∈R,2x>0 |
已知命题p:∃n∈N,2n>1000,则 p为( )
p为( )
| A.∀n∈N,2n≤1000 | B.∀n∈N,2n>1000 |
| C.∃n∈N,2n≤1000 | D.∃n∈N,2n<1000 |
给出下列命题:
①命题“ 的否定是:
的否定是: ;
;
②命题“若 ,则
,则 或
或 ”的否命题是“若
”的否命题是“若 ,则
,则 且
且 ”;
”;
③ 、
、 ,
, ;
;
④向量 ,
, 均是单位向量,其夹角为
均是单位向量,其夹角为 ,则命题“
,则命题“ ”是命题“
”是命题“ ”的充要条件.
”的充要条件.
其中正确的命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
设x∈Z,集合A是奇数集,集合B是偶数集.若命题p:∀x∈A,2x∈B,则( )
A. p:∃x∈A,2x∈B p:∃x∈A,2x∈B |
B. p:∃x∉A,2x∈B p:∃x∉A,2x∈B |
C. p:∃x∈A,2x∉B p:∃x∈A,2x∉B |
D. p:∀x∉A,2x∉B p:∀x∉A,2x∉B |
命题“对任意x∈R,都有x2≥0”的否定为( )
A.存在x0∈R,使得 <0 <0 |
B.对任意x∈R,都有x2<0 |
C.存在x0∈R,使得 ≥0 ≥0 |
D.不存在x∈R,使得x2<0 |