设y1= ,y2=
,y2= ,y3=
,y3= ,则( )
,则( )
| A.y3<y2<y1 | B.y1<y2<y3 | C.y2<y3<y1 | D.y1<y3<y2 |
已知命题p:关于x的函数y=x2﹣3ax+4在[1,+∞)上是增函数,命题q:关于x的函数y=(2a﹣1)x在[1,+∞)上是减函数.若“p且q”为真命题,则实数a的取值范围是( )
A.(﹣∞, ] ] |
B.(0,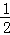 ) ) |
C.(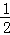 , , ] ] |
D.(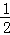 ,1) ,1) |
三个数a=30.2,b=0.23,c=log0.23的大小关系为( )
| A.c<a<b | B.b<a<c | C.a<b<c | D.c<b<a |
已知函数f(x)=4x﹣a•2x+1﹣6,x∈[0,1],
(1)若函数有零点,求a的取值范围;
(2)若不等式f(x)+3a+6≥0恒成立,求a的取值范围.