在三次独立重复试验中,事件A在每次试验中发生的概率相同,若事件A至少发生一次的概率为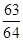 ,则事件A恰好发生一次的概率为( )
,则事件A恰好发生一次的概率为( )
A.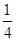 |
B.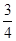 |
C.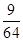 |
D.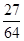 |
设随机变量 服从分布B(n,p),且E
服从分布B(n,p),且E =1.6,D
=1.6,D =1.28则( )
=1.28则( )
| A.n=4,p="0.4" | B.n=5,p=0.32 | C.n=8,p=0.2 | D.n=7,p=0.45 |
在四次独立重复试验中,随机事件A恰好发生1次的概率不大于其恰好发生两次的概率,则事件A在一次试验中发生的概率P的取值范围是( )
A. |
B.[0,0.6] | C.(0,0. 4] | D.[0.6,1) |
已知随机变量ξ的概率分布如下:
| ξ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| P |
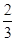 |
 |
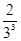 |
 |
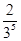 |
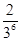 |
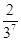 |
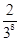 |
 |
m |
则P(ξ=10)等于( )
A、 B、
B、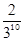 C、
C、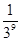 D.、
D.、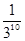
在三次独立重复试验中,事件A在每次试验中发生的概率相同,若事件A至少发生一次的概率为 ,则事件A恰好发生一次的概率为( )
,则事件A恰好发生一次的概率为( )
A. |
B. |
C. |
D. |
在一次反恐演习中,我方三架武装直升机分别从不同方位对同一目标发动攻击(各
发射一枚导弹),由于天气原因,三枚导弹命中目标的概率分别为0.9,0.9,0.8,若至少
有两枚导弹命中目标方可将其摧毁,则目标被摧毁的概率为
| A.0.998 | B.0.046 | C.0.002 | D.0.954 |
位于坐标原点的一个质点P,其移动规则是:质点每次移动一个单位,移动的方向向上或向右,并且向上、向右移动的概率都是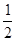 .质点P移动5次后位于点(2,3)的概率是( )
.质点P移动5次后位于点(2,3)的概率是( )
A.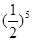 |
B.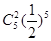 |
C.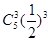 |
D.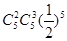 |
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3。设各车主购买保险相互独立.
(Ⅰ)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(Ⅱ)求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率.
抛掷两颗骰子,所得点数之和为ξ,那么ξ=4表示的随机试验结果是( )
A.两颗都是2点
B 一颗是3点,一颗是1点
C.两颗都是4点
D.一颗是3点,一颗是1点或两颗都是2点
下列是4个关于离散型随机变量ξ的期望和方差的描述
①Eξ与Dξ是一个数值,它们是ξ本身所固有的特征数,它们不具有随机性
②若离散型随机变量一切可能取值位于区间内,则a≤Eξ≤b
③离散型随机变量的期望反映了随机变量取值的平均水平,而方差反映的是随机变量取值的稳定与波动,集中与离散的程度
④离散型随机变量的期望值可以是任何实数,而方差的值一定是非负实数
以上4个描述正确的个数是( )
| A.1 | B.2 | C.3 | D.4 |
一次测量中出现正误差和负误差的概率都是 ,则在5次测量中,恰好出现3次正误差的概率是
,则在5次测量中,恰好出现3次正误差的概率是
A. |
B. |
C. |
D. |